O cilindro é um sólido geométrico, estudado na Geometria Espacial, que está presente em vários objetos do nosso dia a dia, como canos, alguns copos, latas de refrigerante, entre outros. Por ser construído por meio da rotação de figuras planas, o cilindro é um sólido geométrico que possui duas bases circulares, classificado como um corpo redondo. Existem cálculos importantes envolvendo o cilindro, como o da área total, da área da base, da área lateral e do volume. Para calcular cada um desses valores, existem fórmulas específicas. Ter as fórmulas em mente facilita os cálculos.
Leia também: Esfera — outro sólido geométrico classificado como corpo redondo
Tópicos deste artigo
- 1 - Resumo sobre cilindro
- 2 - Elementos do cilindro
- 3 - Classificação dos cilindros
- 4 - Planificação do cilindro
- 5 - Áreas do cilindro
- 6 - Volume do cilindro
- 7 - Secção do cilindro
- 8 - Exercícios resolvidos sobre cilindro
Resumo sobre cilindro
-
O cilindro é um sólido geométrico.
-
Possui duas bases circulares paralelas e uma área lateral que conecta essas bases.
-
É um corpo redondo devido às suas bases circulares.
-
São conhecidos dois tipos de cilindro, o cilindro reto e o cilindro oblíquo. Essa classificação se dá de acordo com o eixo.
-
A área da base do cilindro é calculada pela fórmula:
\(A_b=πr^2\)
-
A área lateral do cilindro é calculada pela fórmula:
\(A_l=2πrh\)
-
A área total do cilindro é a soma da área lateral mais 2 vezes a área da base:
\(A_T=2πrh+2πr^2\)
-
O volume do cilindro é calculado pela fórmula:
\(V=πr^2⋅h\)
-
Existem dois tipos de secção que podem ser feitas em um cilindro: transversal e meridiana.
Elementos do cilindro
O cilindro é um sólido geométrico composto por duas bases no formato de círculos e paralelas, e uma área lateral que as conecta. O fato de a base do cilindro ser um círculo faz com que ele seja classificado como corpo redondo. Os principais elementos do cilindro são as suas bases, o comprimento do raio da base, a área lateral e a altura.
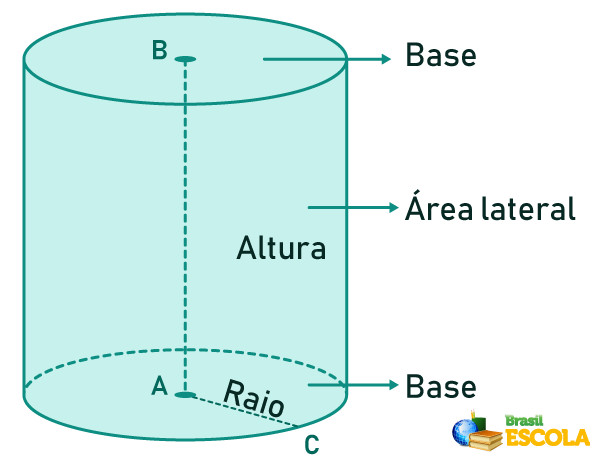
Classificação dos cilindros
Podemos classificar os cilindros entre reto e oblíquio. Veja a seguir.
➝ Cilindro reto
O cilindro é classificado como reto se o eixo for perpendicular às bases do cilindro.
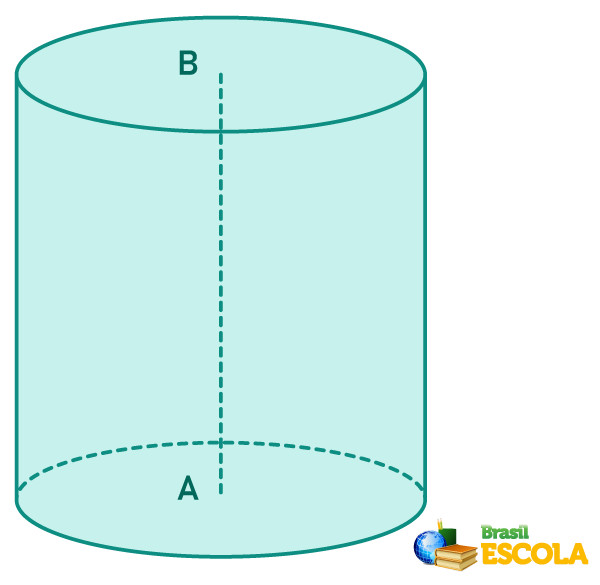
➝ Cilindro oblíquo
O cilindro é classificado como oblíquo se o eixo do cilindro é inclinado.
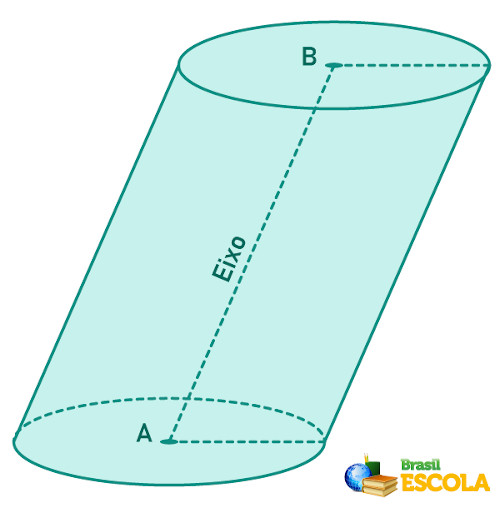
Planificação do cilindro
Para compreender um pouco mais o cálculo da área e do volume do cilindro, é importante reconhecermos a planificação do cilindro.

Ao verificar a planificação do cilindro, é possível perceber que ele é composto por duas circunferências e uma área lateral formada por um retângulo.
Áreas do cilindro
Com a planificação, podemos encontrar a fórmula para calcular a área da base, a área lateral e a área total do cilindro.
➝ Área da base
Como vimos, a base do cilindro é um círculo, então a fórmula da área da base é igual à fórmula da área do círculo.
\(A_b=πr^2\)
-
r → comprimento do raio do cilindro.
Exemplo:
Qual é a área da base de um cilindro que possui raio medindo 4 cm? Utilize 3,1 como aproximação para o valor de π.
Resolução:
Calculando a área da base, temos que r = 4 e \(π=3,1\):
\(A_b=3,1⋅4^2\)
\(A_b=3,1⋅16\)
\(A_b=49,6\ cm^2\)
➝ Área lateral
A área lateral do cilindro é formada por um retângulo, e sabemos que a área de um retângulo é o produto entre a base e a altura. Podemos observar que o comprimento da base do retângulo é igual ao comprimento da circunferência da base do cilindro. Sendo assim, para calcular a base do retângulo, utilizamos a fórmula do comprimento da circunferência. A área lateral pode ser calculada pela fórmula:
\(A_l=2πrh\)
-
h → comprimento da altura do cilindro.
Exemplo:
Um cilindro possui 9 cm de altura e raio medindo 5 cm. Utilizando 3 como aproximação para π, a área lateral desse cilindro é de:
Resolução:
Calculando a área lateral com h = 9, r = 5 e π = 3:
\(A_l=2⋅3⋅5⋅9\)
\(A_l=270\ cm^2\)
➝ Área total
Como o cilindro possui duas bases circulares mais a área lateral, então a área total é a soma dessas áreas.
\(A_T=2A_b+A_l\)
Substituindo pelas fórmulas citadas anteriormente, temos que:
\(A_T=2πr^2+2πrh\)
Podemos ainda colocar \(2πr\) em evidência:
\(A_T=2πr(r+h)\)
Exemplo:
Um cilindro possui altura igual a 12 cm e raio da base igual a 8 cm. Utilizando 3 como aproximação para o valor de π, qual é a área total desse sólido?
Resolução:
Sabemos que h = 12, r = 8 e π = 3, logo:
\(A_T=2⋅3⋅8(8+12)\)
\(A_T=48⋅20\)
\(A_T=960\ cm^2\)
➝ Videoaula sobre área do cilindro
Volume do cilindro
O volume do cilindro é a multiplicação entre a área da base do cilindro e a sua altura. Como já conhecemos a fórmula da área da base, para calcular o volume do cilindro utilizamos a fórmula:
\(V=πr^2⋅h\)
Exemplo:
Qual é o volume de um cilindro que possui raio igual a 7 cm e altura de 10 cm? Utilize 3,14 como aproximação de π.
Resolução:
Calculando o volume, temos que:
\(V=πr^2⋅h\)
\(V=3,14⋅7^2⋅10\)
\(V=3,14⋅49⋅10 \)
\(V=1538,6\ cm³\)
➝ Videoaula sobre volume do cilindro
Secção do cilindro
Podemos realizar uma secção transversal ou uma secção meridional no cilindro. Veja a seguir.
➝ Secção transversal do cilindro
Uma secção transversal divide o cilindro em dois novos cilindros, pois ela é uma secção de um plano paralelo à base do cilindro. A figura formada pelo encontro do plano com o cilindro é um círculo idêntico ao círculo da base do cilindro.
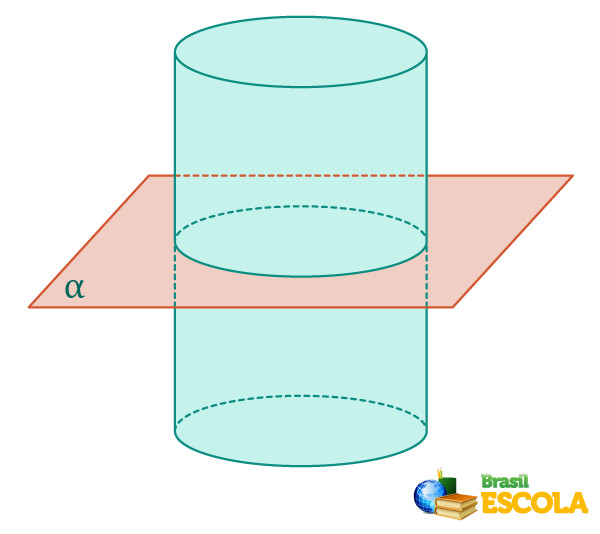
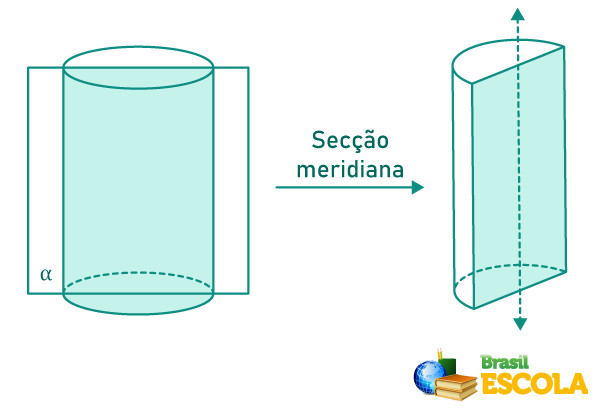
➝ Secção meridiana do cilindro
Uma secção meridiana do cilindro é uma secção de um plano que passa pelo eixo do cilindro formando dois semicilindros.
Saiba mais: Tronco de pirâmide — o sólido geométrico formado após uma secção transversal
Exercícios resolvidos sobre cilindro
Questão 1
(Enem 2015) Uma fábrica brasileira de exportação de peixes vende para o exterior atum em conserva, em dois tipos de latas cilíndricas: uma de altura igual a 4 cm e raio 6 cm, e outra de altura desconhecida e raio de 3 cm, respectivamente, conforme figura. Sabe-se que a medida do volume da lata que possui raio maior, V1, é 1,6 vezes a medida do volume da lata que possui raio menor, V2.
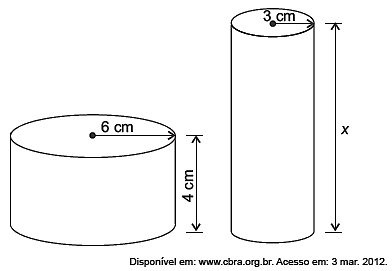
A medida da altura desconhecida vale
A) 8 cm.
B) 10 cm.
C) 16 cm.
D) 20 cm.
E) 40 cm.
Resolução:
Alternativa B
Sabemos que V1 = 1,6V2, então:
\(πr^2 h=1,6πr_2^2⋅h_2\)
\(π⋅6^2⋅4=1,6π⋅3^2⋅x\)
\(π⋅36⋅4=1,6⋅9πx\)
\(144π=14,4πx\)
\(x=\frac{144π}{14,4π}\)
\(x=10\ cm\)
Questão 2
A área total de um cilindro é de 36 m². Sabendo que a circunferência da sua base possui 3,0 metros de diâmetro e considerando π = 3, a altura desse cilindro é de:
A) 1,5 metros
B) 2,0 metros
C) 2,5 metros
D) 3,0 metros
E) 3,5 metros
Resolução:
Alternativa C
Se o diâmetro é de 3,0 metros, então o raio é a metade do diâmetro, ou seja, tem 1,5 metro. Logo:
\(A_T=2πr(r+h)\)
\(36=2⋅3⋅1,5(1,5+h)\)
\(36=6⋅1,5(1,5+h)\)
\(36 =9\ (1,5 +h)\)
\(\frac{36}{9}=1,5+h\)
\(4=1,5 + h\)
\(4-1,5=h\)
\(2,5=h\)
A altura é de 2,5 metros.



