Conjuntos numéricos

O estudo sobre conjuntos numéricos constitui umas das principais áreas da matemática, uma vez que são muito importantes para o próprio desenvolvimento teórico da área e possuem diversas aplicações práticas. Os conjuntos numéricos compreendem em estudar:

• números naturais;

• números inteiros;

• números racionais;

• números irracionais;

• números reais; e

• números complexos.

Leia mais: Números primos – números que têm como divisores apenas o 1 e eles mesmos

Tópicos deste artigo

• 1 - Conjunto dos números naturais
• 2 - Conjunto dos números inteiros
• 3 - Conjunto dos números racionais
• 4 - Conjunto dos números irracionais
• 5 - Conjunto dos números reais
• 6 - Conjunto dos números complexos
• 7 - Intervalos reais

Conjunto dos números naturais

O desenvolvimento das primeiras civilizações trouxe consigo o aprimoramento da agricultura e do comércio e, consequentemente, a utilização de números para representar quantidades. O primeiro conjunto surgiu de maneira natural, daí seu nome. O conjunto nomeado natural é utilizado para representar quantidades, é denotado pelo símbolo ℕ e é escrito em forma de sequência. Veja:

O conjunto dos números naturais é infinito e fechado para as operações de adição e multiplicação, ou seja, sempre que somamos ou multiplicamos dois números naturais, a resposta ainda é natural. Entretanto, para operação de subtração e divisão, o conjunto não é fechado. Veja:

5 – 6 = –1

3 ÷ 2 = 0,5

Note que os números –1 e 0,5 não pertencem ao conjunto dos naturais, e isso é a justificativa para a criação e o estudo de novos conjuntos numéricos.

Ainda, colocando um asterisco (*) no símbolo do conjunto dos naturais, devemos retirar o número zero da listagem, veja:

Conjunto dos números inteiros

O conjunto dos números inteiros surgiu com a necessidade de realizar-se a operação de subtração sem restrições. Como foi visto, ao subtrair-se um número menor de outro maior, a resposta não pertence ao conjunto dos naturais.

O conjunto dos números inteiros também é representado por uma sequência numérica infinita e é denotado pelo símbolo ℤ.

Assim como no conjunto dos números naturais, ao colocar-se um asterisco no símbolo ℤ, o elemento zero é retirado do conjunto, assim:

O símbolo (–) que acompanha um número indica que este é simétrico, assim o simétrico do número 4 é o número –4. Observe também que o conjunto dos números naturais está contido no conjunto dos números inteiros, ou seja, o conjunto dos números naturais é subconjunto do dos números inteiros.

ℕ ⸦ ℤ

Leia também: Operações com números inteiros – quais são e como calcular?

Conjunto dos números racionais

O conjunto dos números racionais é representado pelo símbolo ℚ e não é representado por uma sequência numérica. Esse conjunto é constituído por todos os números que podem ser representados na forma de fração. Representamos seus elementos da seguinte maneira:

Sabemos que todo número inteiro pode ser representado por uma fração, ou seja, o conjunto dos números inteiros está contido no dos números racionais, logo, o conjunto dos números inteiros é subconjunto dos racionais.

ℕ ⸦ ℤ ⸦ ℚ

Os números que possuem representação infinita, como as dízimas periódicas, também possuem representação em forma de fração, desse modo, eles também são racionais.

Leia também: Operações com frações – passo a passo de como as resolver

Conjunto dos números irracionais

Como vimos, um número é racional se ele pode ser escrito na forma de fração. Também foi dito que os números infinitos e periódicos são racionais, no entanto, existem alguns números que não podem ser escritos na forma de uma fração e que, portanto, não pertencem ao conjunto dos números racionais.

Esses números que não são racionais recebem o nome de irracionais e têm como principais características a infinidade da parte decimal e a não periodicidade, ou seja, nenhum número da parte decimal repete-se. Veja alguns exemplos de números irracionais.

• Exemplo 1

As raízes quadradas de números que não são quadrados perfeitos.

• Exemplo 2

Constantes provenientes de razões especiais, como número de ouro, número de Euler ou Pi.

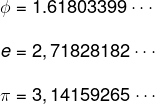
Conjunto dos números reais

O conjunto dos números reais é representado pelo símbolo ℝ e é formado pela união do conjunto dos números racionais com o conjunto dos números irracionais. Lembre-se de que o conjunto dos racionais é a união dos conjuntos naturais e inteiros.

Ao dispormos os números reais em uma reta, temos que o número zero é a origem da reta, à direita do zero estarão os números positivos, e à esquerda, os números negativos.

Como esse eixo é real, podemos dizer que entre dois números existem infinitos números e também que esse eixo é infinito tanto na direção positiva quando na direção negativa.

Conjunto dos números complexos

O conjunto dos números complexos é o mais recente e surgiu pelo mesmo motivo que o conjunto dos números inteiros, ou seja, trata-se de uma operação cujo desenvolvimento somente com o conjunto dos reais não é possível.

Resolvendo a equação a seguir, veja que a ela não possui solução, conhecendo somente os números reais.

x² + 1 = 0

x² = –1

Observe que temos que encontrar um número que, quando elevado ao quadrado, resulte em um número negativo. Sabemos que qualquer número elevado ao quadrado é sempre positivo, logo, esse cálculo não possui solução real.

Assim foram criados os números complexos, em que temos um número imaginário denotado por i, que possui o seguinte valor:

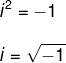
Portanto, perceba que a equação que antes não possuía solução agora a tem. Confira:

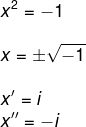
Leia mais: Propriedades envolvendo números complexos

Intervalos reais

Em alguns casos, não vamos utilizar todo eixo real, ou seja, utilizaremos partes dele que serão chamadas de intervalos. Esses intervalos são subconjuntos do conjunto dos números reais. Vamos, a seguir, estabelecer algumas notações para esses subconjuntos.

• Intervalo fechado – sem inclusão dos extremos

Um intervalo é fechado quando ele possui seus dois extremos, ou seja, o mínimo e máximo, e, nesse caso, os extremos não pertencem ao intervalo. Denotaremos isso nos utilizando de uma bolinha aberta. Veja:

Em vermelho estão os números que pertencem a esse intervalo, ou seja, são números maiores que a e menores que b. Algebricamente escrevemos tal intervalo da seguinte maneira:

a < x < b

Em que o número x são todos os números reais que estão nesse intervalo. Podemos também representá-lo de maneira simbólica. Veja:

]a; b[ ou  (a; b)

• Intervalo fechado – com inclusão dos extremos

Agora vamos utilizar bolinhas fechadas para representar que os extremos pertencem ao intervalo.

Assim, estamos colecionando números reais que estão entre a e b, incluindo-os. Algebricamente expressamos tal intervalo por:

a ≤ x ≤ b

Utilizando a notação simbólica, temos:

[a; b]

• Intervalo fechado – incluindo um dos extremos

Ainda tratando de intervalos fechados, temos agora o caso em que somente um dos extremos é incluso. Portanto, uma das bolinhas será fechada, indicando que o número pertence ao intervalo, e a outra não, indicando que o número não pertence a esse intervalo.

Algebricamente representamos esse intervalo da seguinte maneira:

a ≤ x < b

Simbolicamente temos:

[a; b[ ou [a; b)

• Intervalo aberto – sem inclusão do extremo

Um intervalo é aberto quando não possui um elemento máximo ou mínimo. Agora veremos um caso de intervalo aberto que possui apenas elemento máximo, o qual não é incluso no intervalo.

Veja que o intervalo é constituído por números reais menores que b, e observe também que o número b não pertencente ao intervalo (bolinha aberta), assim, algebricamente, podemos representar o intervalo por:

x < b

Simbolicamente podemos representá-lo por:

] – ∞; b[ ou (– ∞; b)

• Intervalo aberto – incluindo o extremo

Outro exemplo de intervalo aberto é o caso em que o extremo é incluso. Aqui temos um intervalo no qual o elemento mínimo aparece, veja:

Note que todos os números reais são maiores ou iguais ao número a, logo, podemos escrever esse intervalo algebricamente por:

x ≥ a

Simbolicamente temos:

[a;  +∞[ ou [a; +∞)

• Intervalo aberto 

Outro caso de intervalo aberto é formado por números maiores e menores que os números fixados na reta real. Veja:

Observe que os números reais que pertencem a esse intervalo são os menores ou iguais ao número a, ou os que são maiores que o número b, logo, temos que:

x  ≤ a ou x > b

Simbolicamente temos:

] – ∞; a] U ] b; + ∞[

ou

(– ∞; a] U ( b; + ∞)