Números racionais

É conhecido como um número racional todo número que pode ser representado como uma fração irredutível. Ao longo da história da humanidade, a ideia de número foi se desenvolvendo gradativamente de acordo com as necessidades humanas. A representação dos números em frações, por exemplo, resolveu problemas que eram solucionados apenas com números inteiros.

Um número racional pode ser representado a partir de uma fração, por isso existem métodos para transformar números inteiros, números decimais exatos e dízimas periódicas em frações.

Leia também: Operações com frações – como resolver?

Tópicos deste artigo

• 1 - Quais são os números racionais?
• 2 - Representação dos números racionais
  • Números inteiros
  • Decimais exatos
  • Dízimas periódicas
  • → 1º caso: fração geratriz de uma dízima periódica simples
  • → 2º caso: fração geratriz de uma dízima periódica composta
• 3 - Propriedades dos números racionais
  • Entre dois números racionais, sempre existirá outro número racional
  • As quatro operações no conjunto dos números racionais são fechadas
• 4 - Subconjuntos dos números racionais

Quais são os números racionais?

Os números racionais são uma ampliação do conjunto dos números inteiros, então, além dos números inteiros, foram acrescentadas todas as frações. O conjunto dos números racionais é representado por:

O que essa representação diz é que um número é racional se ele pode ser representado como a fração a sobre b, tal que a é um número inteiro e b é um número inteiro diferente de zero. Mas se formos definir os números racionais com menos rigor, podemos dizer o seguinte:

Satisfazem essa definição:

• os números inteiros, por exemplo: -10, 7, 0;

• os números decimais exatos, por exemplo: 1,25; 0,1; 3,1415;

• as dízimas periódicas simples, por exemplo: 1,424242…;

• as dízimas periódicas compostas, por exemplo: 1,0288888…

Não são números racionais:

• As dízimas não periódicas, por exemplo: 4,1239489201…;

• As raízes não exatas, por exemplo: ;

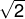• A raiz quadrada de números negativos, por exemplo: .

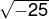Observação: A existência de números não racionais faz com que surjam outros conjuntos, como o dos números irracionais e o dos números complexos.

Representação dos números racionais

Entendendo que a fração é uma divisão de dois números inteiros, para ser um número racional, é possível representar esse número como fração. Logo cada um dos casos citados anteriormente como números racionais (os números inteiros, os decimais exatos e as dízimas periódicas) pode ser representado como uma fração.

• Números inteiros

Existem infinitas possibilidades para a representação de um número inteiro como uma fração, já que uma fração pode ser representada na forma irredutível ou não.

Exemplos:

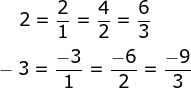
• Decimais exatos

Para transformar um número decimal exato em uma fração, contamos a quantidade de números que há na sua parte decimal, ou seja, depois da vírgula. Se houver um número após a vírgula, escreveremos a parte inteira mais a parte decimal sem a vírgula sobre 10. Se houver dois números na parte decimal sobre 100, na prática, a quantidade de números na parte decimal será a quantidade de zeros que teremos no denominador. Veja o exemplo:

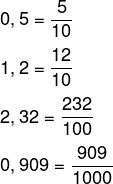
• Dízimas periódicas

Encontrar a representação fracionária de uma dízima nem sempre é uma tarefa fácil, o que chamamos de fração geratriz. Para facilitar esse trabalho, foi observado que, na equação que utilizamos para encontrar a fração geratriz, existem regularidades, o que permitiu o desenvolvimento de um método prático.

Em primeiro lugar, precisamos entender que existem dois tipos de dízima periódica, a simples e a composta. Uma dízima é simples se, em sua parte decimal, existir somente a parte que se repete, ou seja, o período. Uma dízima é composta se, em sua parte decimal, existir uma parte não periódica.

Exemplo:

9,323232… → dízima periódica simples
Parte inteira é igual a 9.
Período é igual a 32.

8,7151515… → dízima periódica composta
Parte inteira é igual a 8.
Parte decimal não periódica é igual a 7.
Período é igual a 15.

Veja também: Frações equivalentes – frações que representam a mesma quantidade

→ 1º caso: fração geratriz de uma dízima periódica simples

No primeiro caso, para transformar uma dízima periódica simples em fração pelo método prático, basta escrever a parte inteira mais o período sem a vírgula no numerador. No denominador, para cada elemento na parte periódica, acrescentamos um 9.

Exemplo:

A fração geratriz de 9,323232… , como vimos, possui período igual a 32, ou seja, dois números no seu período, sendo assim, o denominador é 99. A parte inteira mais a parte periódica sem a vírgula é 932, e a parte inteira é 9. A diferença entre 932 e 9 será o nosso denominador, então temos que: Então, a fração geratriz dessa dízima é:

\(\frac{932-9}{99}=\frac{923}{99}\)

→ 2º caso: fração geratriz de uma dízima periódica composta

A dízima periódica composta é um pouco mais trabalhosa. Vamos encontrar a fração geratriz da dízima que trabalhamos no exemplo.

8,7151515… → dízima periódica composta.

Parte inteira é igual a 8.

Parte decimal não periódica é igual a 7.

Parte decimal do período é igual a 15.

O numerador será a subtração 8715 – 87, ou seja, a diferença entre o número que vai da parte inteira até a parte periódica com a parte que se não repete da dízima.

O numerador será igual a 8715 – 87 = 8628.

Já para encontrar o denominador, vamos analisar a parte decimal. Primeiro vamos ver a parte decimal não periódica e periódica. Nesse caso, a parte decimal do número é 715. Para cada número que está na parte periódica, vamos acrescentar um 9 no início do denominador. Como a parte periódica nesse caso possui dois números (15), haverá dois 9 no denominador. Para cada número na parte decimal que não for periódico, acrescentaremos um 0 no final do denominador, que será 990.

Logo, a fração geratriz da dízima será:

Propriedades dos números racionais

• Entre dois números racionais, sempre existirá outro número racional

É interessante pensarmos nessa propriedade, que foi muito discutida pelos povos antigos, tornando-se um paradoxo. Escolhendo dois números racionais, sempre existirá um número entre eles.

Exemplo:

Entre o 1 e o 2, existe o 1,5; entre o 1 e o 1,5, existe o 1,25; entre o 1 e o 1,25, existe o 1,125 e assim sucessivamente. Por mais que eu escolha dois números racionais com uma diferença muito pequena entre eles, é sempre possível encontrar um número racional entre eles. Essa propriedade torna impossível definirmos sucessor e antecessor nos números racionais.

• As quatro operações no conjunto dos números racionais são fechadas

Dizemos que o conjunto é fechado para a soma, por exemplo, se a soma de dois números racionais sempre gerar como resposta outro número racional. É o que acontece com as quatro operações em Q.

A soma, a subtração, a divisão e a multiplicação entre dois números racionais sempre resultarão em um número racional. Na verdade, até mesmo a potenciação de um número racional sempre vai gerar como resposta um número racional.

O conjunto dos números racionais não é fechado para a radiciação. Assim, mesmo 2 sendo um número racional, a raiz quadrada de 2 é um número irracional.

Veja também: Frações equivalentes – frações que representam a mesma quantidade

Subconjuntos dos números racionais

Conhecemos como subconjuntos ou relação de inclusão os conjuntos formados por elementos que pertencem ao conjunto dos números racionais. Existem vários subconjuntos possíveis, como o conjunto dos números inteiros ou dos naturais, pois todo número inteiro é racional, assim como todo número natural é racional.

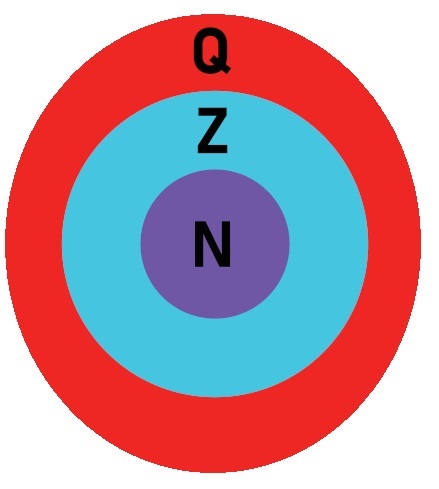
Exemplo:

Conjunto dos números inteiros: Z= {…-3, -2, -1, 0,1, 2, 3, …}.

Quando isso acontece, dizemos que Z ⸦ Q (lê-se: Z está contido em Q ou o conjunto dos números inteiros está contido no conjunto dos números racionais.)

Existem alguns símbolos que são essenciais para a criação de subconjuntos de Q, sendo eles: +,- e *, que significam, respectivamente, positivos, negativos e não nulos.

Exemplos:

Q* → (lê-se: conjunto dos números racionais não nulos.)

Q₊ → (lê-se: conjunto dos números racionais positivos.)

Q_- → (lê-se: conjunto dos números racionais negativos.)

Q^*₊ → (lê-se: conjunto dos números racionais positivos e não nulos.)

Q^*_- → (lê-se: conjunto dos números racionais negativos e não nulos.)

Note que todos esses conjuntos são subconjuntos de Q, pois todos os elementos pertencem ao conjunto dos números racionais. Além dos conjuntos apresentados, podemos trabalhar com vários subconjuntos em Q, como o conjunto formado por números ímpares, ou primos, ou pares, enfim, há várias e várias possibilidades de subconjuntos.