Os números inteiros são os números que não possuem parte decimal. Esse conjunto é formado pelos números naturais e os números opostos aos naturais, ou seja, os números negativos, logo um número é inteiro se ele não apresenta parte decimal. Eles podem ser representados desta forma:
ℤ = {... - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, ...}.
Os números inteiros também podem ser representados na reta numérica. Nesse caso, o zero fica no centro; à direita do zero, os números positivos; à esquerda, os números negativos.
Leia também: Quais são os conjuntos numéricos?
Tópicos deste artigo
- 1 - O que são números inteiros?
- 2 - Representação dos números inteiros na reta
- 3 - Comparação de dois números inteiros
- 4 - Subconjuntos dos números inteiros (ℤ)
- 5 - Operações com números inteiros
- 6 - Exercícios resolvidos sobre números inteiros
O que são números inteiros?
Os números inteiros surgiram a partir de uma ampliação do conjunto dos números naturais, pois só os números naturais não eram suficientes para resolver certas situações cotidianas, passando a ser necessário utilizar os números negativos opostos aos números naturais, como o – 1, – 2, –3 e assim sucessivamente.
Os números inteiros, conhecidos também como conjunto dos números inteiros, representados pela letra grega ℤ, são os números positivos e negativos que não possuem nenhuma parte decimal. De modo geral, podemos listar os números inteiros deste modo:
ℤ = {... - 4, - 3, - 2, - 1, 0, 1, 2, 3, 4, ...}
Representação dos números inteiros na reta
Podemos representar os números inteiros na reta. Cada número inteiro é um ponto da reta. No centro da reta, está o número 0; à direita, os inteiros positivos; à esquerda, os inteiros negativos.
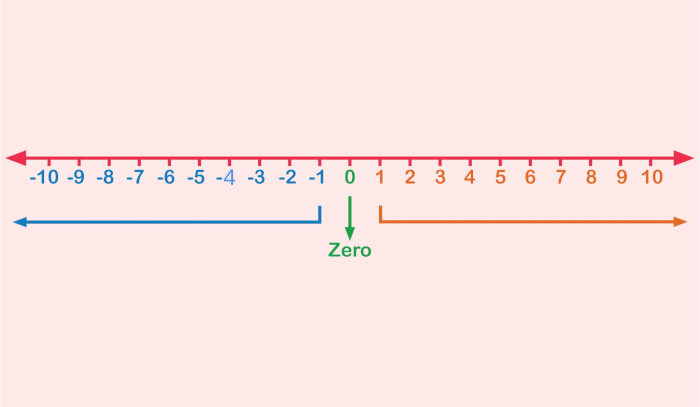
Comparação de dois números inteiros
Quando comparamos dois números inteiros, podemos separar quatro casos:
1. Comparando um número inteiro com o zero, sabemos que o zero é maior que qualquer número positivo e menor que qualquer número negativo.
- 0 > – 5 (Zero é maior que menos cinco.)
- –2 < 0 (Menos dois é menor que zero.)
- 25 > 0 (Vinte e cinco é maior que zero.)
- 0 < 10 (Zero é menor que dez.)
2. Um número positivo é sempre maior que um número negativo, e um número negativo é sempre menor que um número positivo.
Exemplos:
- 5 > – 8 (Cinco é maior que menos oito.)
- 12 > – 4 (Doze é maior que menos quatro.)
- – 1 < 1 (Menos um é menor que um.)
- – 9 < 4 (Menos nove é menor que quatro.)
3. Quando comparamos dois números positivos, o maior deles é o que está mais distante do zero.
Exemplos:
- 5 > 3 (Cinco é maior que três.)
- 3 > 2 (Três é maior que dois.)
- 4 < 9 (Quatro é menor do que nove.)
- 20 < 50 (Vinte é menor que cinquenta.)
4. Quando comparamos dois números negativos, o maior deles é o que está mais próximo do zero.
Exemplos:
- –12 < – 9 (Menos doze é menor que menos nove.)
- – 42 < – 30 (Menos quarenta e dois é menor que menos trinta.)
- – 1 > – 5 (Menos um é maior que menos cinco.)
- – 16 > – 20 (Menos dezesseis é menor que menos vinte.)
Leia também: Números racionais — a ampliação do conjunto dos números inteiros
Subconjuntos dos números inteiros (ℤ)
Os subconjuntos dos números inteiros são:
- ℤ*: são os números inteiros, exceto o zero.
ℤ* = {..., – 3, – 2, – 1, 1, 2, 3, 4, ...}
- ℤ+: são os números inteiros não negativos.
ℤ+ = {0, 1, 2, 3, 4, ...}
- ℤ_: são os números inteiros não positivos.
ℤ_= {..., – 4, – 3, – 2,-1, 0}
- ℤ*+: são os números inteiros não negativos e sem o zero.
ℤ*+ = {1,2,3,4, 5...}
- ℤ*_: são os números inteiros, com exceção dos positivos e do zero.
ℤ*_= {..., – 4, – 3, – 2, – 1}
Operações com números inteiros
⇒ Adição de números inteiros
A adição de números inteiros pode ser separada em dois casos: quando ambos os números são positivos ou quando ambos são negativos. Ao contrário da multiplicação e da divisão, a adição e subtração não requerem a aplicação das regras do "jogo de sinais".
No primeiro cenário, quando os números têm o mesmo sinal, basta somar as parcelas e manter o sinal.
Exemplos:
- +7 + 3 = 10
- – 5 + (– 2) = – 7
Agora, no segundo cenário, quando os números têm sinais opostos, subtraímos e preservamos o sinal do número com maior valor absoluto.
Exemplos:
- – 8 + 11 = +3 (porque 11 – 8 = 3, e o valor absoluto de 11 é maior que o de 8, então a resposta é positiva).
- +6 + (– 9) = – 3 (porque 9 – 6 = 3, e o valor absoluto de 9 é maior que o de 6, então a resposta é negativa).
⇒ Subtração de números inteiros
Para efetuar subtrações, as regras são semelhantes às usadas na adição, porém, antes de tudo, devemos escrever o oposto da segunda parcela.
Exemplos:
- + 6 – (+ 3)
Para resolver, temos que – (+ 3) é o mesmo que calcular o inverso de +3, ou seja –3.
+ 6 – 3 = + 3
Então podemos concluir que + 6 – (+ 3) = 3.
- 9 – (– 5)
Temos que – (– 5) é o oposto de – 5, o que resulta em +5. Em seguida, realizamos a operação:
9 + 5 = 14
Então podemos concluir que 9 – (– 5) = 14.
⇒ Multiplicação e divisão de números inteiros
Tanto na multiplicação quanto na divisão entre dois números inteiros, é necessário fazer jogo de sinal e posteriormente realizar a operação como ela é feita entre números naturais.
Veja a tabela com o jogo de sinais a seguir:
|
+ |
+ |
= |
+ |
|
– |
– |
= |
+ |
|
+ |
– |
= |
– |
|
– |
+ |
= |
– |
Em resumo, quando os sinais forem iguais, a resposta será positiva; quando os sinais forem diferentes, a resposta será negativa.
Exemplos:
- (– 6) × (– 7) = + 42 (Ambos negativos, então sinais iguais e produto positivo.)
- (– 5) × (+ 4) = – 20 (Números têm sinais opostos, logo o produto é negativo.)
- (+ 8) × (– 3) = – 24 (Números têm sinais opostos, logo o produto é negativo.)
- (+ 9) × (+ 2) = + 18 (Ambos positivos, então sinais iguais e produto positivo.)
- (– 16) ÷ (– 4) = + 4 (Ambos negativos, então sinais iguais e quociente positivo.)
- (– 20) ÷ (+5) = – 4 (Números têm sinais opostos, logo o quociente é negativo.)
- (+ 15) ÷ (– 3) = – 5 (Números têm sinais opostos, logo o quociente é negativo.)
- (+36) ÷ (+6) = +6 (Ambos positivos, então sinais iguais e quociente positivo)
Leia também: Números reais — o conjunto que engloba os números racionais e irracionais
Exercícios resolvidos sobre números inteiros
Questão 1
No dia 05, Kárita recebeu o seu salário, de R$ 3500,00. Nesse mesmo dia, ela pagou a escola do seu filho, que lhe custa R$ 615,00. Posteriormente, ela fez as compras do supermercado e gastou um total de R$ 555,00. Depois disso, no dia 10, ela pagou o condomínio, que custa R$ 310,00. Quanto ainda resta do seu salário?
A) R$ 3000,00
B) R$ 2020,00
C) R$ 1950,00
D) R$ 1860,00
E) R$ 1710,00
Resolução:
Alternativa B.
3500 – 615 – 555 – 310 = 2020
Questão 2
Analise as expressões numéricas a seguir que envolvem números inteiros:
I. (– 3 + 4) × 2
II. (– 6 – 4) : 5
III. – 3 × (– 5) + 4
IV. 8 : (-2) – 1
Tem como resultado um número inteiro negativo:
A) somente I.
B) somente II.
C) somente I e II.
D) somente II e IV.
E) somente III e IV.
Resolução:
Alternativa D.
I. (– 3 + 4) × 2 = 1× 2 = 2
II. (– 6 – 4) : 5 = – 10 : 5 = – 2
III. – 3 × (– 5) + 4 = +15 + 4 = 19
IV. 8 : (-2) – 1 = – 4 – 1 = – 5
Fontes:
IEZZI, Gelson; MURAKAMI, Carlos. Fundamentos da Matemática Elementar, Volume 1, Funções, São Paulo: Editora Atual, 8ª Edição, 2004


