Números primos

Números primos são todos os números naturais que possuem somente dois divisores: 1 e eles mesmos. Existem vários números primos, como os números 2, 3, 5, 7, 11. Para saber se o número é primo, é necessário analisar quais são os seus divisores. Se ele possuir somente dois divisores, então ele será primo. Para encontrar números primos, foi desenvolvido o crivo de Eratóstenes, e o outro método é utilizar a fatoração do número.

Os números primos são utilizados em criptografia, na fatoração de números naturais, entre outras situações. O que fascina os matemáticos é que não existe uma sequência ou uma progressão que facilite encontrar um número primo, logo, estudiosos se dedicam por anos a fim de encontrar números primos maiores.

Leia também: O que são números inteiros?

Tópicos deste artigo

• 1 - Resumo sobre números primos
• 2 - Videoaula sobre números primos
• 3 - O que são números primos?
• 4 - Como saber se um número é primo?
  • → Métodos para identificar números primos
  • → Crivo de Eratóstenes
• 5 - Quais são os números primos?
• 6 - Criptografia e números primos
• 7 - Curiosidades sobre números primos
• 8 - Exercícios resolvidos sobre os números primos

Números inteiros

Saiba mais

Números irracionais

Saiba mais

Resumo sobre números primos

• Números primos são números que podem ser divididos apenas por 1 e eles mesmos.
• Para encontrar um número primo, podemos utilizar o crivo de Eratóstenes.
• Para saber se um número é primo ou não, é necessário verificar quais são os divisores desse número.
• Existem matemáticos que se dedicam a encontrar os maiores números primos possíveis.

Videoaula sobre números primos

O que são números primos?

Os números primos são números naturais que possuem apenas dois divisores positivos diferentes: o número 1 e eles mesmos. Em outras palavras, um número primo só pode ser dividido exatamente por 1 e por ele próprio, sem deixar resto.

Como saber se um número é primo?

Para saber se um número é primo, é necessário checar quais são os seus divisores, então um número que, em sua lista de divisores, possuir números além do 1 e de si próprio não será primo. Agora, se o número tiver somente dois divisores, no caso 1 e ele mesmo, então ele será um número primo.

Exemplo:

Vamos analisar se os números 17 e 27 são primos:

D(17) = {1, 17}

D(27) = {1, 3, 9, 27}

Analisando os divisores, afirmamos que 17 é um número primo e 27 não é um número primo.

Note que 17 possui somente dois divisores, sendo assim, ele será um número primo. Agora, ao analisar o número 27, sabemos que ele é divisível por 1, por ele mesmo, por 3 e por 9; como ele tem 4 divisores, então não é um número primo.

Veremos, a seguir, dois métodos utilizados para encontrar números primos.

→ Métodos para identificar números primos

• Fatoração 

De modo geral, para descobrir se um número é primo ou não, podemos realizar a fatoração desse número. Todo número pode ser descrito como o produto entre números primos.

Exemplo 1:

Vamos verificar se o número 84 é um número primo:

Primeiro, vamos montar o algoritmo e encontrar o menor número primo que divide o número 84, que, no caso, é o número 2:

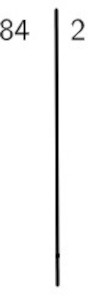
Posteriormente dividimos 84 por 2 e escrevemos o resultado abaixo do 84:

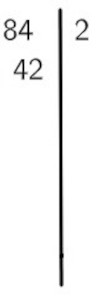
Já pelo fato de 84 ser divisível por 2, podemos descartar a chance de ele ser primo, pois tem mais de 2 divisores. Para terminar a fatoração, repetimos o processo até encontrar 1 como resultado da divisão:

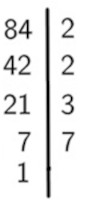
Por fim, podemos reescrever o 84 como o produto dos divisores:

84 = 2²·3·7

Note que o número 84 foi escrito como o produto de números primos.

Exemplo 2:

Vamos verificar se o número 19 é um número primo:

A fim de decompô-lo em fatores primos, dividindo-o por 2, 3, 5, 7, 11, 13 e 17, podemos verificar que ele não é divisível por nenhum desses números primos, sendo assim, 19 é divisível só por ele mesmo e por 1.

19 : 19 = 1

Portanto, 19 é um número primo.

→ Crivo de Eratóstenes

Achar quais são os números primos pode ser trabalhoso. O método mais usado para essa tarefa é o crivo de Eratóstenes, que nos permite encontrar todos os números primos entre dois números. Faremos, por exemplo, a lista com todos os números primos de 1 até 100. Para começar, vamos listar esses números:

Primeiro sabemos que o número 1 não é primo, pois ele possui somente 1 divisor. Além disso, sabemos que todos os números pares são divisíveis por 2, e 2 é primo por possuir 2 divisores, porém, os demais números pares não são primos, então riscaremos eles da lista.

Dos números restantes, sabemos que o próximo primo é o número 3, então vamos tirar da lista todos os que são múltiplos de 3 e maiores que o próprio 3:

O próximo número primo é o 5, os múltiplos de 5 são números terminados em 0 e 5, então nos resta tirar da lista todos os números terminados em 5.

Repetindo o processo, retiraremos da lista os números múltiplos de 7:

Agora, sabendo que 11 é primo, note que, como não há nenhum número múltiplo de 11 que não tenha sido retirado da lista, sabemos então que terminamos o crivo, e os números primos são os números que não foram retirados da lista:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.

Veja também: Critérios de divisibilidade — regras fundamentais dessa operação que você precisa conhecer

Quais são os números primos?

Existem infinitos números primos, o único número primo par que existe é o 2, os demais são todos ímpares. Veremos, a seguir, todos os números primos menores que 1000.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.

Criptografia e números primos

Os números primos têm um papel fundamental na segurança das informações que trocamos na internet. Eles são usados em sistemas de criptografia, que garantem que mensagens, senhas e dados bancários sejam protegidos. A criptografia é como um código secreto usado para transformar informações em algo que só pode ser lido por quem tem a chave correta. A criptografia embaralha as informações, e só quem tem a chave pode desembaralhar.

Os números primos desempenham um papel fundamental no método de criptografia chamado RSA, um dos mais conhecidos. Esse método se baseia em propriedades únicas dos números primos para criar chaves que protegem informações. O processo começa com a escolha de dois números primos grandes. Por exemplo, utilizaremos os números 61 e 67. Os números utilizados são muito maiores na prática, com centenas de dígitos, entretanto, esses números foram escolhidos para facilitar o exemplo. Esses dois números primos são multiplicados, e o resultado dessa multiplicação 61 × 67 = 4087 se torna a base de um bloqueio que protege os dados.

A segurança desse método está na dificuldade de encontrar quais números foram multiplicados para termos 4087 como resultado, ou seja, se alguém tiver apenas o número 4087, será difícil descobrir que ele foi formado pelos primos 61 e 67. Esse processo de encontrar os fatores da multiplicação, para encontrar os primos que geraram o número, leva tanto tempo e exige tanto poder computacional que torna a criptografia segura, especialmente quando os números primos utilizados são grandes.

Os números primos são a base para a criptografia pela dificuldade de se encontrar a chave certa para desbloquear as informações, ou seja, os fatores que foram multiplicados.

Saiba mais: Como encontrar o máximo divisor comum (MDC) entre dois números

Curiosidades sobre números primos

• O número 2 é o único número primo par, os demais são todos ímpares, afinal, todo número par é divisível por 2.
• O número 1 não é primo, pois possui somente 1 divisor.
• Existem infinitos números primos.
• Dois números são conhecidos como primos entre si quando não possuem nenhum divisor em comum, por exemplo 8 e 15. O 8 ou o 15 não possuem nenhum divisor em comum, logo, eles são primos entre si.
• Primos gêmeos são pares de números primos que têm uma diferença de 2 unidades entre eles, como 11 e 13, ou 17 e 19.

Exercícios resolvidos sobre os números primos

Questão 1

Sobre os números primos, é correto afirmar que:
A) Todo número ímpar é primo.
B) O número 1 é considerado primo.
C) Existe apenas um número primo par.
D) Não existem números primos maiores que 100.

Resolução:

Alternativa C

De fato, existe apenas um número primo par, o número 2, logo, a alternativa correta é a alternativa C. Além disso, sabemos que nem todo número ímpar é primo, pois há números ímpares que possuem mais de 1 divisor, o que torna a alternativa A incorreta. O número 1 não é um número primo, logo, a alternativa B está incorreta, pois ele só possui um único divisor. Sendo assim, também sabemos que os primos são infinitos, o que torna a alternativa D incorreta.

Questão 2

Um professor de matemática propôs a seguinte sequência: 2, 3, 5, 7, 11, 13, 17... Qual das alternativas abaixo corresponde à soma dos três próximos números primos dessa sequência?

A) 66
B) 70
C) 71
D) 74

Resolução:

Alternativa C

Primeiro vamos listar os próximos números primos, que, no caso, são 19, 23 e 29.

Agora, basta calcular a soma deles:

19 + 23 + 29 = 71

Fontes

BURTON, David M. Introdução à teoria dos números. 7. ed. São Paulo: Pearson Prentice Hall, 2002.

HARDY, G. H.; WRIGHT, E. M. Introdução à Teoria dos Números. 6. ed. Oxford: Oxford University Press, 2008.