Operações matemáticas básicas

As operações básicas em Matemática são os processos mais elementares realizados entre números: a adição, subtração, multiplicação e divisão. Cada uma dessas operações possui propriedades que podem ser exploradas para facilitar cálculos.

Uma observação importante ao resolver operações matemáticas é identificar em qual conjunto estão os elementos trabalhados. Considere que, ao longo deste texto, todos os números são reais. Para o estudo de números inteiros, leia os artigos específicos para cada operação básica indicados ao final da página.

Leia também: Quais são os conjuntos numéricos?

Tópicos deste artigo

• 1 - Resumo sobre operações matemáticas básicas
• 2 - Quais são as operações matemáticas básicas?
  • ? Adição
  • ? Subtração
  • ? Multiplicação
  • ? Divisão
• 3 - Exercícios resolvidos sobre operações matemáticas básicas

Resumo sobre operações matemáticas básicas

• Adição, subtração, multiplicação e divisão são as operações matemáticas básicas.

• A subtração é a operação inversa da adição, e a divisão é a operação inversa da multiplicação.

• O resultado de uma adição é a soma, e o resultado de uma subtração é a diferença.

• O resultado de uma multiplicação é o produto, e o resultado de uma divisão é o quociente.

Quais são as operações matemáticas básicas?

As operações matemáticas básicas são adição, subtração, multiplicação e divisão. Cabe destacar duas relações entre essas operações:

• A subtração é a operação inversa da adição.

• A divisão é a operação inversa da multiplicação.

Vamos conhecer um pouco mais sobre cada uma e, ao final do texto, resolver alguns problemas associados às operações básicas.

➝ Adição

A operação de adição envolve adicionar, acrescentar, juntar. Essa operação é indicada pelo símbolo + e possui a seguinte estrutura:

$a+b=c$

em que c é a soma das parcelas a e b. Lemos “a mais b é igual a c”. Lembrando que a, b e c representam números reais.

Exemplos:

$1+2=3$

$24+30=54$

$-1+7=6$

$1,25+2=2,25$

$x+x=2x$

Observação: A reta numérica é uma importante ferramenta para o estudo da adição.

• Propriedades da adição

• Comutatividade: se a e b são números reais, então $a+b=b+a$.

Ou seja, a ordem das parcelas não altera a soma. Observe que, por exemplo, $3+10=13\ e\ 10+3=13$.

• Associatividade: se a, b e c são números reais, então $a+(b+c)=(a+b)+c$.

Observe que, por exemplo, $2+(1+3)=2+4=6$ e $(2+1)+3=3+3=6$.

• Elemento neutro: o elemento 0 é neutro para a operação de adição. Ou seja, se a  é um número real, então a+0=a .

Observe que, por exemplo, $7+0=7$.

• Elemento oposto (ou simétrico): se a é um número real, então $-a$ é chamado de elemento oposto a a e $a+(-a)=0$.

Observe que, por exemplo, $5+(-5)=0$.

Observação: Para compreender a última propriedade e resolver diferentes problemas relacionados às quatro operações básicas, é fundamental conhecer a regra de sinais.   

➝ Subtração

A operação de subtração envolve subtrair, retirar, remover. Essa operação é indicada pelo símbolo $\mathbf{-}$ e possui a seguinte estrutura:

$a-b=c$

em que c é a diferença entre a e b. Lemos “a menos b é igual a c”.

Exemplos:

$6-1=5$

$32-11=21$

$- 4-3=-7$

$10,5-4,75=5,75$

$8z-z=7z$

Observação: A reta numérica também pode ser utilizada para o estudo da subtração.

➝ Multiplicação

A operação de multiplicação envolve multiplicar, avolumar. Essa operação é indicada por diferentes símbolos, como $×$, $*$ e $\cdot$ e possui a seguinte estrutura:

$a×b=c$

em que c é o produto entre os fatores a e b. Lemos “a vezes b é igual a c”.

Exemplos:

$2 ×3 =6$

$4×(-2)=-8$

$x*x=x^2$

•  

• Propriedades da multiplicação

• • Comutatividade: se a e b são números reais, então $a×b=b×a$.

Ou seja, a ordem dos fatores não altera o produto. Observe que, por exemplo, $- 9×2=- 18$ e $2×- 9 =- 18$.

• • Distributividade: se a, b e c são números reais, então $a×(b+c)=a×b+a×c$.

Observe que, por exemplo, $3×(9+4)=3×13=39$ e $3×9+3×4=27+12=39$.

Essa propriedade (conhecida como “chuveirinho”) também é válida em relação à subtração, ou seja, $a×(b-c)=a×b-a×c$.

• • Associatividade: se a, b e c são números reais, então $a×(b×c)=(a×b)×c$.

Observe que, por exemplo, $10×(5×8)=10×40=400$ e $(10×5)×8=50×8=400$.

• • Elemento neutro: o elemento 1 é neutro para a operação de multiplicação. Ou seja, se a  é um número real, então $a×1=a$.

Observe que, por exemplo, $2×1=2$.

• • Elemento inverso: se a  é um número real, então $\frac{1}a$ é chamado de inverso multiplicativo de a e $a×\frac{1}a=1$.

Por exemplo, $6×\frac{1}6=1$.

➝ Divisão

A operação de divisão envolve dividir, fragmentar, segmentar. Essa operação é indicada pelo símbolo $÷$ e possui a seguinte estrutura:

$a÷b=c$

em que b é diferente de zero e c é o quociente ou razão entre a e b. Lemos “a dividido por b é igual a c”.

Uma divisão pode ser exata quando o resultado é um número inteiro ou não exata quando o resultado não é um número inteiro.

É importante observar que se $a÷b=c$, então $b×c=a$.

Exemplos:

$27÷9=3$

$20÷8=2,5$

$3,2÷1,6=2$

$12x÷4=3x$

Leia também: Como resolver operações com frações?

Exercícios resolvidos sobre operações matemáticas básicas

Questão 1

(Enem 2022) Uma instituição de ensino superior ofereceu vagas em um processo seletivo de acesso a seus cursos. Finalizadas as inscrições, foi divulgada a relação do número de candidatos por vaga em cada um dos cursos oferecidos. Esses dados são apresentados no quadro.

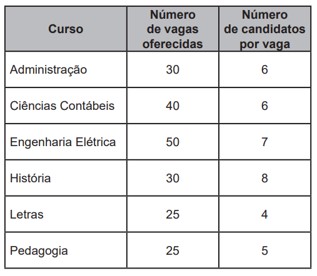
Qual foi o número total de candidatos inscritos nesse processo seletivo?

a) 200

b) 400

c) 1200

d) 1235

e) 7200

Resolução

Alternativa D

O número total de candidatos inscritos no processo seletivo é dado pela soma do número de candidatos inscritos para cada curso. E essa informação é obtida pelo produto entre o número de vagas oferecidas e o número de candidatos por vaga.

• Administração: $30×6=180$ candidatos inscritos.

• Ciências Contábeis: $40×6=240$ candidatos inscritos.

• Engenharia Elétrica: $50×7=350$ candidatos inscritos.

• História: $30×8=240$ candidatos inscritos.

• Letras: $25×4=100$ candidatos inscritos.

• Pedagogia: $25×5=125$ candidatos inscritos.

Portanto, o número de candidatos inscritos no processo seletivo foi de $180+240+350+240+100+125=1235$.

Questão 2

(Enem 2016 — adaptado) O quadro apresenta a ordem de colocação dos seis primeiros países em um dia de disputa nas Olimpíadas. A ordenação é feita de acordo com as quantidades de medalhas de ouro, prata e bronze, respectivamente.

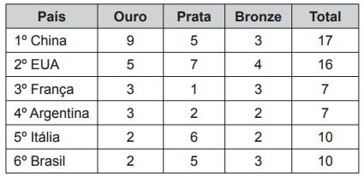
Qual país conquistou 3 medalhas a mais do que França e Argentina juntas?

a) China.

b) EUA

c) Itália

d) Brasil

Resolução

Alternativa A

Perceba que, juntas, França e Argentina conquistaram 14 medalhas $(7+7=14 )$.

Observe que:

• China conquistou 17 medalhas, ou seja, 3 medalhas a mais do que França e Argentina juntas $(17-14=3 )$.

• EUA conquistou 16 medalhas, ou seja, 2 medalhas a mais do que França e Argentina juntas $(16-14=2 )$.

• Itália conquistou 10 medalhas, ou seja, 4 medalhas a menos do que França e Argentina juntas $(10-14=-4 )$.

• Brasil conquistou 10 medalhas, ou seja, 4 medalhas a menos do que França e Argentina juntas $(10-14=-4 )$.

 

Por Maria Luiza Alves Rizzo
Professora de Matemática