Fração geratriz

 A fração geratriz é a representação fracionária de uma dízima periódica. Essa representação é uma estratégia importante na resolução de problemas sobre operações básicas da Matemática que envolvem dízimas periódicas. Para encontrá-la, podemos utilizar técnicas de equação e também um método prático.

Leia também: Como resolver operações com fração?

Tópicos deste artigo

• 1 - O que é uma dízima periódica?
• 2 - O que é fração geratriz?
• 3 - Passo a passo para calcular a fração geratriz
  • Dízimas periódicas simples
  • Dízima periódica composta
• 4 - Método prático
  • Método prático para dízimas periódicas simples
  • Método prático para dízimas periódicas compostas
• 5 - Exercícios resolvidos

O que é uma dízima periódica?

Antes de entender o que é uma fração geratriz, é fundamental compreender o que é uma dízima periódica. Existem dois casos possíveis de dízimas periódicas: a dízima periódica simples e a dízima periódica composta. Uma dízima periódica é um número decimal que possui parte decimal infinita e periódica.

• Dízima periódica simples

A dízima periódica simples é composta pela parte inteira e parte decimal. A parte decimal é a repetição do seu período, conforme os exemplos a seguir.

Exemplos:

a) 1,2222…

Parte inteira → 1
Parte decimal → 0,2222…
Período → 2

b) 3,252525…

Parte inteira → 3
Parte decimal → 0,252525…
Período → 25

c) 0,8888…

Parte inteira → 0
Parte decimal → 0,8888
Período → 8

• Dízima periódica composta

A dízima periódica composta é uma dízima que possui parte inteira, parte decimal e, em sua parte decimal, uma parte não periódica — conhecida como antiperíodo — e o período.

Exemplos:

a) 2,0666…

Parte inteira → 2
Parte decimal → 0,0666…
Antiperíodo → 0
Período → 6

b) 13,518888…

Parte inteira → 13
Parte decimal → 0,51888…
Antiperíodo → 51
Período → 8

c) 0,109090909…

Parte inteira → 0
Parte decimal → 0,10909090
Antiperíodo → 1
Período → 09

Leia também: O que são frações equivalentes?

O que é fração geratriz?

Fração geratriz é a representação fracionária da dízima periódica, seja ela simples, seja composta. Como o nome sugere, a fração geratriz gera a dízima quando dividimos o numerador pelo denominador da representação fracionária.

Exemplos:

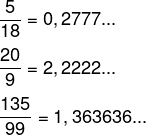
Passo a passo para calcular a fração geratriz

Vejamos o passo a passo para a dízima periódica simples e para a dízima periódica composta.

• Dízimas periódicas simples

Para encontrar a fração geratriz de uma dízima periódica simples, é necessário seguir alguns passos, sendo eles:

• 1º passo: igualar a dízima periódica a x.

• 2º passo: de acordo com a quantidade de algarismos do período, multiplicar os dois lados da equação por:

• 10 → se houver 1 algarismo no período;

• 100 → se houver 2 algarismos no período;

• 1000 → se houver 3 algarismos no período; e assim sucessivamente.

• 3º passo: calcular a diferença entre a equação encontrada no 2º passo e a equação igualada a x no 1º passo, e resolver a equação.

Exemplo 1:

Encontre a fração geratriz da dízima 1,444…

x = 1,4444…

O período é 4 e, como há apenas um algarismo no período, multiplicaremos por 10 dos dois lados:

10x = 1,444… · 10
10x = 14,444…

10x – x = 14,444.. – 0,444…
9x = 14
x = 14/9

Então, a fração geratriz da dízima é:

Exemplo 2:

Encontre a fração geratriz da dízima periódica 3,252525…

x = 3,252525…

O período é 25 e, como possui 2 algarismos, multiplicaremos por 100.

100x = 3,252525… · 100
100x = 325,252525…

Agora calculando a diferença entre 100x e x:

100x – x = 325,2525… – 3,252525…
99x = 322
x = 322/99

Então, a fração geratriz da dízima é:

• Dízima periódica composta

Quando a dízima periódica é composta, o que muda é que acrescentamos um novo passo na resolução para encontrar a fração geratriz.

• 1º passo: igualar a dízima periódica a x.

• 2º passo: transformar a dízima periódica composta em uma dízima periódica simples multiplicando por:

• 10, se houver 1 algarismo no antiperíodo;

• 100, se houver 2 algarismos no antiperíodo; e assim sucessivamente.

• 3º passo: de acordo com a quantidade de algarismos do período, multiplicar os dois lados da equação por:

• 10 → se houver 1 algarismo no período;

• 100 → se houver 2 algarismos no período;

• 1000 → se houver 3 algarismos no período; e assim sucessivamente.

• 4º passo: calcular a diferença entre a equação encontrada no 3º passo e 2º passo, e resolver a equação.

Exemplo:

Encontre a fração geratriz da dízima 5,0323232…

x = 5,0323232…

Note que há 1 algarismo no antiperíodo, que é o 0. Multiplicaremos por 10 para que ela vire uma dízima periódica.

10x = 5,0323232… · 10
10x = 50,323232…

Agora vamos identificar o período, que é 32. Como há 2 algarismos, multiplicaremos a dízima por 100.

1000x = 5032,323232…

Agora calculamos a diferença entre 1000x e 10x:

1000x – 10x = 5032,323232… – 50,323232…
990x = 4982
x=4982/990

Então, a fração geratriz é:

Veja também: Como é formado um número misto?

Método prático

Utilizamos o método prático para facilitar o processo de encontrar a fração geratriz da dízima periódica. Vamos analisar dois casos diferentes: quando a dízima periódica é simples e quando ela é composta.

• Método prático para dízimas periódicas simples

Em uma dízima periódica simples, o método prático consiste em:

• 1º passo: escrever a soma entre a parte inteira e a parte decimal da dízima periódica;

• 2º passo: transformar a parte decimal em fração, da seguinte maneira: o numerador sempre será o período e o denominador será:

• 9 → se houver 1 algarismo no período;

• 99 → se houver 2 algarismos no período;

• 999 → se houver 3 algarismos no período; e assim sucessivamente.

• 3º passo: realizar a soma da parte inteira com a fração encontrada.

Exemplo:

5,888…

5,888… = 5 + 0,888…

Transformando 0,888… em fração, temos numerador igual a 8, pois 8 é o período da fração, e denominador igual a 9, pois há somente 1 algarismo no período, logo:

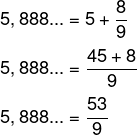
• Método prático para dízimas periódicas compostas

Exemplo:

Encontraremos a fração geratriz da dízima 4,1252525…

Primeiro identificamos a parte inteira, o antiperíodo e o período da dízima composta:

 Parte inteira: 4

Antiperíodo: 1

Período: 25 

O numerador da dízima composta é a diferença entre o número formado pelos algarismos da parte inteira, antiperíodo e período, com o número formado pela parte inteira e antiperíodo.

4125 – 41 = 4084

No denominador, para cada número no período, acrescentamos um 9 e, na sequência, para cada número na parte não periódica, um 0.

O período é 25, então acrescentamos 99; o antiperíodo é 1, então acrescentamos 0, logo o denominador é 990.

A fração geratriz da dízima é:

Exercícios resolvidos

Questão 1 - Ao realizar a divisão entre dois números naturais, foi encontrada a dízima periódica 1,353535… A fração geratriz dessa dízima é:

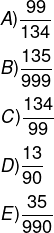
Resolução

Alternativa C.

Faremos x = 1,353535…

Multiplicando por 100 dos dois lados, temos que:

100 x = 135,3535…

Agora calcularemos a diferença entre 100x e x.

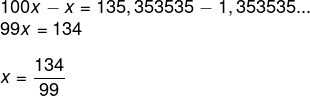
Questão 2 - Se x = 0,151515… e y = 0,242424…, a divisão y : x é igual a?

Resolução

Alternativa A.

Encontrando as frações geratrizes pelo método prático, temos que:

x = 0,151515…

A dízima possui período igual a 15, logo seu numerador é 15, e o denominador, 99.

Com o mesmo raciocínio para y = 0,242424…, o numerador é 24, e o denominador, 99.

  

Por Raul Rodrigues de Oliveira
Professor de Matemática