Divisão

A divisão é uma das quatro operações básicas da matemática e é inversa à multiplicação. A divisão de um número consiste em seu fracionamento, na sua fragmentação, que pode ter como resultado um número inteiro ou um número decimal.

Assim como as outras operações fundamentais da matemática, a divisão também está muito presente em nosso cotidiano, por isso, é essencial conhecer bem esse processo, a fim de adquirir prática e tornar esse cálculo mais ágil.

Tópicos deste artigo

• 1 - Elementos da divisão
• 2 - Passo a passo da divisão
• 3 - Jogo de sinais na divisão
  • → Exemplos
• 4 - Divisão com vírgula
  • Divisão em que o quociente não é inteiro
  • Divisão em que o dividendo e o divisor não são inteiros
  • → Exemplo
• 5 - Exercício resolvido

Elementos da divisão

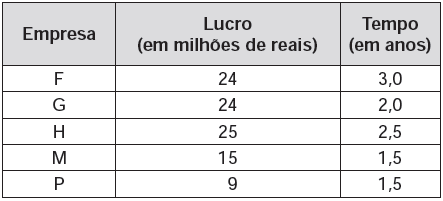
Quando vamos dividir um número P por um número d, devemos buscar um número q que multiplicado por d seja igual a P. Cada um desses elementos recebem um nome: P é chamado de dividendo, d é o divisor e q o quociente.

Nem sempre é possível encontrar esse número q, em alguns casos, a multiplicação de d por q apenas fica muito próxima de P. Nessas situações, a diferença de P pelo resultado da multiplicação de d por q é chamado de resto e será denotado por r.

→ Exemplos

a) 28: 2  = 14, pois 2 ·14  = 28 → Divisão exata

b) 29: 2 ≠ 14, pois 2 ·14 = 28 → Divisão não exata, apresenta resto = 1

Quando o resto não aparece, ou seja, quando r = 0, dizemos que o número P é divisível por d. Caso contrário, P não é divisível por d.

Podemos afirmar que:

P = d ·q + r

Vejamos agora um método que facilita encontrar todos esses elementos: método da chave. Veja a figura abaixo:

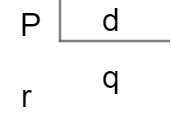
→ Exemplo

Na divisão do número 25 por 5 temos:

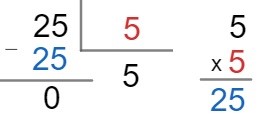
O número 25 é o dividendo, o número 5 é o divisor, 5 é o quociente, e zero é o resto da divisão. Note que para realizar a divisão é necessário encontrar um número que multiplicado por 5 seja igual a 25, nesse caso, o número é o próprio 5.

Veja também que podemos escrever o número 25 da seguinte maneira:

25 = 5 · 5 + 0

Veja também: Critérios de divisibilidade: regras que auxiliam o cálculo de divisão

Passo a passo da divisão

Para facilitar o processo de divisão, temos um algoritmo, isto é, temos um passo a passo que pode facilitar. Para verificarmos esse processo, vamos tomar a seguinte divisão 64: 4.

Primeiro passo: montar a operação utilizando o método da chave.

Segundo passo: tentar encontrar um número que multiplicado por 4 seja igual a 64. Como essa não é uma tarefa fácil, vamos tomar somente o número 6 para dividir com o número 4, ou seja, o algarismo da dezena. Assim, devemos determinar um número inteiro que multiplicado por 4 seja igual a 6 ou que chegue o mais próximo possível. Veja:

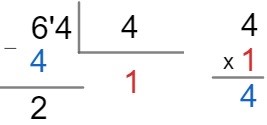
Terceiro passo: prosseguir a divisão descendo o algarismo da unidade, que não foi dividido, nesse caso, o 4. Veja:

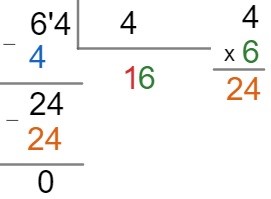
O processo chega ao fim, quando obtemos que o resto é igual a 0. Caso contrário, devemos continuar a divisão seguindo os mesmos procedimentos.

Leia também: Dicas e macetes para cálculos de divisão

Jogo de sinais na divisão

Na divisão de números inteiros, devemos ficar atentos quanto aos sinais. Devemos lembrar-nos das propriedades dos números inteiros:

→ Exemplos

a) (+ 55) : (+11) = +5

b) (+243) : (– 3) = – 81

c) (– 1050) : (+5) = – 210

d) (– 12) : (– 6) = +2

Divisão com vírgula

Na divisão, há duas situações em que a vírgula pode aparecer: a primeira é quando o quociente não é um número inteiro, e a segunda é quando o dividendo e o divisor não são inteiros. Vejamos como resolver cada um desses casos por meio de exemplos.

Divisão em que o quociente não é inteiro

Esse caso ocorre quando os números não são divisíveis, ou seja, o resto da divisão é um número diferente de zero. Para realizar a divisão, devemos seguir o mesmo passo a passo citado anteriormente.

Entretanto, quando o resto for um número que não pode mais ser dividido, devemos acrescentar uma vírgula no quociente e um zero na casa das unidades do resto.

Veja:

A divisão entre o número 55 e 2 não é exata, pois 55 não é par, então, vamos realizar a divisão e encontrar o resultado seguindo o passo a passo.

Observe que o resto da divisão é diferente de zero e não é possível dividi-lo pelo quociente. O segundo passo consiste em acrescentar uma vírgula no quociente e um zero no resto na casa da unidade.

Então:

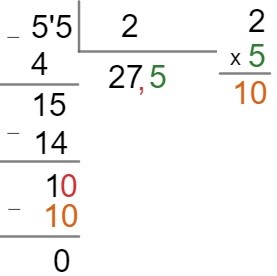
Veja que após acrescentar a vírgula e o número zero a operação de divisão seguiu novamente o passo a passo.

Divisão em que o dividendo e o divisor não são inteiros

Primeiro passo: eliminar a vírgula do dividendo e do divisor.

Para que isso possa ocorrer, deve-se andar a mesma quantidade de casas decimais tanto no divisor quanto no dividendo. Isso é permitido, pois a divisão nada mais é que uma fração em que o dividendo é o numerador e o divisor é o denominador. Dessa forma, podemos multiplicar o dividendo e o divisor por potências de 10, que é o equivalente a andar casas decimais.

Segundo passo: seguir o passo a passo apresentado anteriormente.

→ Exemplo

Vamos dividir o número 0,05 por 0,2 seguindo o passo a passo.

Devemos andar 2 casas decimais para que a vírgula desapareça do dividendo, logo devemos andar 2 casas decimais também no divisor, ou seja, vamos multiplicar o divisor e o dividendo por 100.

0,05 ·100 = 5

0,2 ·100 = 20

Agora a divisão fica:

Para começar a fazer a divisão, devemos encontrar um número que multiplicado por 20 seja igual a 5, porém esse número inteiro não existe! Então, acrescentamos 0 e uma vírgula no quociente, 0 no dividendo e prosseguimos a divisão normalmente.

Lembrete: após o processo de colocar a vírgula no quociente, podemos colocar o número 0 na casa da unidade sempre que for necessário.

Leia também: Divisão com frações: saiba como calcular

Exercício resolvido

Questão 1 – João vai fazer uma viagem de 521 quilômetros. Para fazer a viagem com mais segurança, ele decidiu realizá-la em duas etapas. Quantos quilômetros João viajará por dia?

Solução

O total da viagem é de 521 quilômetros e vai ser realizado em 2 dias, para determinar a quantidade de quilômetros que será rodado por dia devemos dividir esses números.

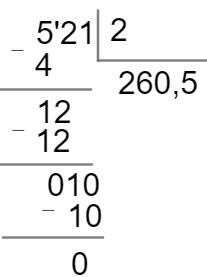
Portanto, João vai viajar 260,5 quilômetros por dia.

 

Por L.do Robson Luiz

Professor de Matemática