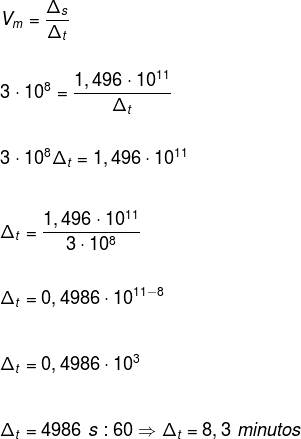Notação científica

A notação científica é uma ferramenta bastante utilizada não só na Matemática, mas também na Física e Química. Ela nos permite escrever e operar números que, quando escritos em sua forma original, exigem grande paciência e esforço, já que, ou são números muito grandes, ou muito pequenos. Imagine, por exemplo, você escrevendo a distância entre o planeta Terra e o Sol em quilômetros ou escrevendo a carga de um próton em coulomb.

Neste texto, vamos explicar como representar esses números de uma maneira mais simples e algumas de suas características.

Leia também: Unidades astronômicas: quais são?

Como transformar um número em notação científica

Para transformar um número em notação científica, é necessário entender o que são potências de base 10. Da definição de potência, temos que:

10⁰ = 1

10¹ = 10

10² = 10 · 10 = 100

10³ = 10 · 10 · 10 = 1.000

10⁴ = 10 · 10· 10· 10 = 10.000

10⁵ = 10· 10· 10· 10· 10 = 100.000

Observe que, na medida em que o expoente aumenta, também aumenta a quantidade de zeros da resposta. Veja também que o número que está no expoente é a quantidade de zeros que temos à direita. Isso é equivalente a dizer que a quantidade de casas decimais andadas para a direita é igual ao expoente da potência. Por exemplo, 10¹⁰ é igual a 10.000.000.000

Outro caso que devemos analisar é quando o expoente é um número negativo.

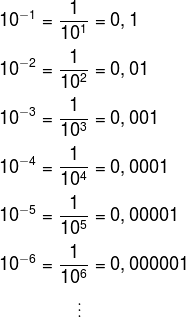
Observe que, quando o expoente é negativo, as casas decimais aparecem à esquerda do número, isto é, “andamos” casas decimais para a esquerda. Veja também que a quantidade de casas decimais andadas para esquerda coincide com o expoente da potência. A quantidade de zeros à esquerda do número 1 coincide, portanto, com o número do expoente. A potência 10 ^–10 , por exemplo, é igual a 0,0000000001.

Revisada a ideia de potência de base 10, vamos agora entender como transformar um número em notação científica. É importante ressaltar que, independentemente do número, para escrevê-lo na forma de notação científica, devemos sempre deixá-lo com um algarismo significativo.

Assim, para escrever um número na forma de notação científica, o primeiro passo é escrevê-lo em forma de produto, de forma que apareça uma potência de base 10 (forma decimal). Veja os exemplos:

a) 0,0000034 = 3,4 · 0,000001 = 3,4 · 10 ^{– 6}

b) 134.000.000.000 = 134 · 1.000.000.000 = 134 · 10⁹

Convenhamos que esse processo não é nada prático, então, a fim de facilitá-lo, note que, quando “andamos” com a vírgula para a direita, o expoente da base 10 diminui a quantidade de casas decimais andadas. Agora, quando “andamos” casas decimais para esquerda, o expoente da base 10 aumenta a quantidade de casas andadas.

Em resumo, se os zeros estiverem à esquerda do número, o expoente é negativo e coincide com a quantidade de zeros; se os zeros aparecerem à direita do número, o expoente é positivo e também coincide com a quantidade de zeros.

Exemplos

a) A distância entre o planeta Terra e o Sol é de 149.600.000 km.

Observe o número e veja que, para escrevê-lo em notação científica, é necessário “andar” com a vírgula oito casas decimais para esquerda, logo o expoente da base 10 será positivo:

149.600.000 = 1,496 · 10⁸

b) A idade aproximada do planeta Terra é de 4.543.000.000 anos.

De modo análogo, veja que, para escrever o número em notação científica, é necessário andar 9 casas decimais para a esquerda, logo:

4.543.000.000 = 4,543· 10⁹

c) O diâmetro de um átomo é da ordem de 1 nanômetro, ou seja, 0,0000000001.

Para escrever esse número utilizando a notação científica, devemos andar 10 casas decimais para a direita, logo:

0,0000000001 = 1 · 10^-10

Leia também: Sistema Internacional de Unidades: a padronização das unidades de medida

Tópicos deste artigo

• 1 - Operações com notação científica
• 2 - Exercícios resolvidos

Operações com notação científica

Para operar dois números escritos em notação científica, temos inicialmente que operar os números que acompanham as potências de 10 e, em seguida, operar as potências de 10. Para isso, é necessário ter em mente as propriedades das potências. As mais utilizadas são:

• Produto de potências de mesma base:

a^m ·aⁿ = a^{m + n}

• Quociente de potências de mesma base:

• Potência de uma potência:

(a^m)ⁿ = a^{m ·n}

Exemplos

a) 0,00003 · 0,0027

Sabemos que 0,00003 = 3 · 10 ^{– 5} e que 0,0027 = 27 · 10 ^{– 4} , então, temos que:

0,00003 · 0,0027

3 · 10 ^{– 5} · 27 · 10 ^{– 4}

(3 · 27) · 10 ^{– 5 + (– 4)}

81· 10 ^{– 9}

0,000000081

b) 0,0000055 : 11.000.000.000

Vamos escrever os números utilizando a notação científica, logo 0,0000055 = 55 · 10 ^{– 7} e 11.000.000.000 = 11 · 10⁹.

0,0000055 : 11.000.000.000

55 · 10 ^{– 7} : 11 · 10⁹

(55 : 11) · 10 ^{(– 7 – 9)}

5 · 10 ^{– 16}

0,0000000000000005

Exercícios resolvidos

Questão 1 – (UFRGS) Considerando um próton como um cubo de aresta 10 ^{– 11} m e massa 10 ^{– 21} kg, qual a sua densidade?

Solução

Sabemos que a densidade é a razão entre massa e volume, logo é necessário calcular o volume desse próton. Como a forma do próton segundo o enunciado é um cubo, o volume é determinado por: V = a³, em que a é a medida da aresta.

V = (10 ^{– 11})³

V = 10 ^{– 33} m³

A densidade é, portanto:

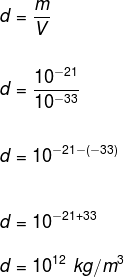
Questão 2 – A velocidade da luz é de 3,0 · 10⁸ m/s. A distância entre a Terra e o Sol é de 149.600.000 km. Quanto tempo a luz do sol gasta para chegar até a Terra?

Solução

Sabemos que a relação entre distância, velocidade e tempo é determinada por:

Antes de substituir os valores na fórmula, note que a velocidade da luz está em metros por segundo, e a distância entre a Terra e o Sol, em quilômetros, ou seja, é necessário escrever essa distância em metros. Para isso, vamos multiplicar a distância por 1000.

149.600.000 · 1000

1,496 · 10⁸ · 10³

1,496 · 10⁸⁺³

1,496 · 10¹¹ m

Agora, substituindo os valores na fórmula, temos:

Por Robson Luiz
Professor de Matemática