O resto da divisão

A divisão é uma das quatro operações fundamentais da matemática. Dividimos com o objetivo de partir ou separar em diversas partes, ao dividirmos um número por outro podemos gerar resto ou não, caso o resto seja zero, a divisão é exata, se não for, então a divisão é não exata.

Relembre a estrutura do algoritmo da divisão:

O algoritmo da divisão pode ainda ser estruturado da seguinte forma:

D = d . q + r

D = Dividendo
d = Divisor
q = Quociente
r = Resto

Em toda a divisão, o valor numérico do resto sempre será menor que o número referente ao divisor.

Resto < Divisor
r < d → (Lê-se: O resto é menor que o divisor)

Resolveremos quatro exemplos a fim de entender melhor o que é o resto para a divisão exata e não exata.

Exemplo 1

Encontre o resto da divisão, se houver.

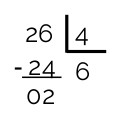
Para verificar se a divisão está correta, faça:

D = d . q + r
D = 4 . 6 + 2
D = 26

Dividendo = 26; Divisor = 4; Resto = 2, Quociente = 6

O resto da divisão de 26 por 4 é 2; essa é uma divisão não exata

Exemplo 2

Descubra o resto da divisão de 243 por 5 e diga se a divisão é exata ou não exata.

Na divisão de 243 por 5, o resto é 3. Essa é uma divisão não exata. Para tirar a prova real, faça:

D = d . q + r
D = 5 . 48 + 3
D = 243

Dividendo = 243; Divisor = 5; Resto = 3, Quociente = 48

Exemplo 3
A divisão do número 124 pelo número 2 é exata ou não exata?

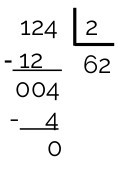
Essa divisão é exata porque o resto é zero.

Exemplo 4

O professor de história precisa organizar 50 alunos em grupos, de forma que esses grupos possuam a mesma quantidade de alunos. Como ele deverá proceder?

Para solucionar esse exemplo devemos encontrar os divisores de 50.

Divisores de 50 = { 1, 2, 5, 10, 25, 50}

Podemos verificar que em todos os casos de divisão o resto é zero, sendo assim, a divisão é exata.

Reposta final: O professor poderá organizar os alunos em 2, 5, 10 ou em 25 grupos.

Por Naysa Oliveira
Graduada em Matemática