O que é dízima periódica?

Dízimas periódicas são números infinitos e periódicos. Infinitos, pois eles não possuem fim, e periódicos, pois certas partes deles se repetem, isto é, possuem um período. Além disso, as dízimas periódicas podem ser representadas na forma fracionária, ou seja, podemos dizer que elas são números racionais.

Se dividirmos o numerador de uma fração pelo denominador e encontrarmos uma dízima, então essa fração será chamada de fração geratriz. As dízimas podem ser classificadas como simples e compostas.

Leia também: Curiosidades sobre a divisão de números naturais

Tópicos deste artigo

• 1 - Tipos de dízimas periódicas
• 2 - Fração geratriz

Tipos de dízimas periódicas

• Dízima periódica simples           

É caracterizada por não possuir antiperíodo, ou seja, o período (parte que se repete) vem logo depois da vírgula. Veja alguns exemplos:

• Exemplos

a) 0,32323232…

Período → 32

b) 0,111111…

Período → 1

c) 0,543543543…

Período → 543

d) 6,987698769876…

Período → 9876

Observação: Podemos representar uma dízima periódica com uma barra em cima do período, por exemplo o número 6,98769876… pode ser escrito da seguinte maneira:

• Dízima periódica composta

É aquela que possui antiperíodo, ou seja, entre a vírgula e o período existe um número que não se repete.

• Exemplos

a) 2,3244444444…

Período → 4

Antiperíodo → 32

b) 9,123656565…

Período → 65

Antiperíodo → 123

c) 0, 876547654…

Período → 7654

Antiperíodo → 8

Fração geratriz

As dízimas periódicas podem ser representadas na forma de fração, o que faz delas números racionais. Quando uma fração gera uma dízima periódica, ela recebe o nome de fração geratriz. O processo para encontrar a fração geratriz é simples, acompanhe o passo a passo:

• Exemplo 1

A dízima utilizada no exemplo será: 0,323232…

Passo 1 – Nomeie a dízima como uma incógnita.

x = 0,323232…

Passo 2 – Utilize o princípio da equivalência, ou seja, se operarmos em um lado da igualdade, devemos realizar a mesma operação do outro lado para manter a equivalência. Dessa forma, vamos multiplicar a dízima por uma potência de 10 até que o período fique antes da vírgula.

Observe que o período nesse caso é 32, então devemos fazer a multiplicação por 100. Perceba também que a quantidade de dígitos do período fornece-nos a quantidade de zeros que a potência de 10 deve ter. Dessa forma:

100 · x = 0,323232… · 100

100x  = 32,32323232…

Passo 3 – Subtraia a equação do passo 2 da equação do passo 1.

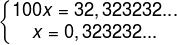
Subtraindo termo a termo, temos:

100x – x = 32,323232… – 0,323232…

99x = 32

Veja agora o exemplo em que se aplica o método para dízimas compostas.

Leia também: Propriedades da multiplicação que facilitam o cálculo mental

• Exemplo 2

A dízima composta utilizada será: 9,123656565….

Antes de realizar o primeiro passo, note que:

9,123656565… = 9 + 0, 123656565…

Vamos trabalhar somente com a dízima, e, ao final, basta somar 9 à fração geratriz.

Passo 1 – Nomeie a dízima como uma incógnita.

x = 0,123656565…

Passo 2 – Multiplique-a por uma potência de 10 até que a parte não periódica fique antes da vírgula. Nesse caso, a multiplicação deve ser por 100, pois a parte não periódica possui três dígitos.

100 · x = 0,123656565… ·100

100x = 123,656565…

Passo 3 – Multiplique-a novamente por uma potência de 10 até que a parte periódica fique antes da vírgula. Como a parte periódica (65) possui dois dígitos, multiplicamos ambos os lados por 100, assim:

100 ·100x = 123,656565… ·100

10000x = 12365,656565…

Passo 4 – Por fim, subtraia a equação obtida no passo 3 da equação obtida no passo 2.

10000x – 100x = 12365,656565… – 123,656565…

9.900 x = 12.242

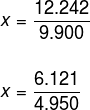
Lembre-se de que ainda é necessário somar 9 a essa fração, logo:

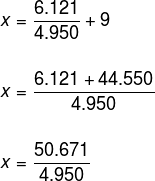
Por Robson Luiz
Professor de Matemática