O máximo divisor comum (MDC) é o maior número que é divisor de dois ou mais números simultaneamente. Para encontrá-lo, podemos escrever a lista de divisores de cada um desses números e compará-las, buscando o maior divisor em comum entre esses números. Existem, todavia, outros métodos para encontrar o MDC: o método de decomposição simultânea desses números ou a decomposição em fatores primos.
Leia também: Múltiplos e divisores — dois conceitos que você precisa entender
Tópicos deste artigo
- 1 - Resumo sobre MDC
- 2 - Videoaula sobre MDC
- 3 - O que é o MDC?
- 4 - Como calcular o MDC?
- 5 - Propriedades do MDC
- 6 - Diferença entre MDC e MMC
- 7 - Exercícios resolvidos sobre MDC
Resumo sobre MDC
-
O máximo divisor comum (MDC) é o maior número que divide dois ou mais números ao mesmo tempo.
-
Utilizamos o MDC para resolver situações-problema envolvendo divisores.
-
Para encontrar o MDC, existem diferentes métodos.
Videoaula sobre MDC
O que é o MDC?
MDC é o máximo divisor comum entre dois ou mais números, ou seja, o maior número que divide dois ou mais números simultaneamente. Dados dois números, como o 8 e o 16, sabemos que eles possuem divisores em comum, a saber: 1, 2, 4 e 8, que dividem tanto o 8 quanto o 16 ao mesmo tempo, logo:
MDC (8,16) = 8, que é o maior deles.
Como calcular o MDC?
Existem diferentes métodos para calcular o MDC entre dois ou mais números. Os mais comuns são o método da comparação entre os divisores, a decomposição em fatores primos e a decomposição simultânea.
-
Método da comparação
O método da comparação consiste em escrever a lista dos divisores de cada um dos números e encontrar qual é o maior divisor em comum entre eles.
Exemplo:
Encontre o MDC de 20 e 16.
Por comparação, vamos escrever os divisores de 20 e os divisores de 16.
D(20) = {1,2,4,5,10,20}
D(12)= {1,2,4,8,16}
Existem alguns divisores em comum, que são os números {1,2,4}. O MDC é o maior deles.
MDC (20,16) = 4
O problema é que esse método nem sempre é conveniente, pois, se os números forem muito grandes, encontrar os divisores de cada um deles pode não ser uma tarefa fácil.
Leia também: Propriedades da multiplicação que facilitam o cálculo mental
-
Método da decomposição
O método da decomposição consiste em decompor os números em fatores primos e procurar quais são os fatores em comum entre esses dois números.
Exemplo:
Encontre o MDC entre 120 e 150.
Primeiro encontraremos a decomposição em fatores primos de cada um desses números:
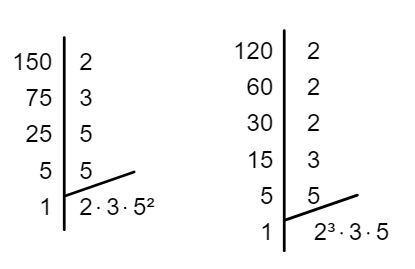
Agora vamos encontrar os fatores que são comuns aos dois e calcular o produto entre eles.
Note que, em 150, aparece o fator 2 e, em 120, aparece 2³. Nesse caso, sempre escolhemos o fator com o menor expoente, ou seja, 2 é um fator em comum. O mesmo acontece com o 3 e com o 5.
MDC (150, 120) = 2 · 3 · 5 = 30
-
Decomposição simultânea
Semelhantemente ao método anterior, a ideia é encontrar os fatores em comum aos dois números quando realizamos a decomposição; porém, faremos essa decomposição dos dois números ao mesmo tempo.
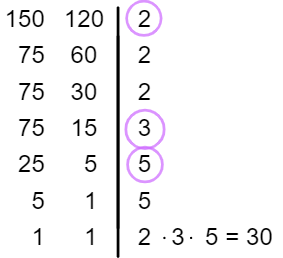
Propriedades do MDC
O máximo divisor comum possui propriedades importantes que nos auxiliam a encontrar de forma mais rápida o MDC entre dois números.
-
1ª propriedade: o MDC entre dois números consecutivos é sempre igual a 1. Exemplo:
MDC (10, 11) = 1
-
2ª propriedade: quando temos dois ou mais números e um dos números é divisor dos demais, então ele é o MDC. Exemplo:
MDC (5,10,15)
Sabemos que o 5 é divisor de 10 e de 15, então:
MDC (5,10,15) = 5
Leia também: Critérios de divisibilidade — conhecê-los facilita bastante o cálculo da divisão
Diferença entre MDC e MMC
Além do máximo divisor comum, existe também o mínimo múltiplo comum, conhecido como MMC, que é o menor múltiplo em comum que dois ou mais números possuem.
As diferenças entre eles é que, no MDC, estamos calculando o maior divisor em comum; já no MMC, estamos trabalhando com o menor múltiplo em comum.
Exemplo 1:
Dados os números 32 e 24, encontre o MDC entre eles.
-
1º passo: vamos listar os divisores de 32 e os divisores de 24.
D(32) = {1,2,4,8,16, 32}
D(24) = {1,2,3,4,6,8, 12, 24}
-
2º passo: agora encontraremos o maior número que divide ambos ao mesmo tempo.
MDC (32,24) = 8
Oito é o maior número que divide 32 e 24 ao mesmo tempo.
Exemplo 2:
Dados os números 24 e 32, encontre o MMC entre eles.
Vamos listar os múltiplos de 24 e de 32 até encontrar um que seja comum aos dois.
M(24) = {0, 24, 48, 72, 96 ...}
M(32) = {0, 32, 64, 96 …}
MMC(24,32) = 96
Exercícios resolvidos sobre MDC
Questão 1
(Enem 2015) O gerente de um cinema fornece anualmente ingressos gratuitos para escolas. Este ano, serão distribuídos 400 ingressos para uma sessão vespertina e 320 ingressos para uma sessão noturna de um mesmo filme. Várias escolas podem ser escolhidas para receberem ingressos. Há alguns critérios para a distribuição dos ingressos:
1) cada escola deverá receber ingressos para uma única sessão;
2) todas as escolas contempladas deverão receber o mesmo número de ingressos;
3) não haverá sobra de ingressos (ou seja, todos os ingressos serão distribuídos).
O número mínimo de escolas que podem ser escolhidas para obter ingressos, segundo os critérios estabelecidos, é:
A) 2.
B) 4.
C) 9.
D) 40.
E) 80.
Resolução:
Alternativa C.
Calculando o MDC entre 320 e 400, temos que:

Para encontrar o MDC, vamos multiplicar os números que são divisores tanto de 320 quanto de 400:
MDC (400, 320) = 24 · 5 = 16 · 5 = 80
Cada escola receberá 80 ingressos, logo 720 : 80 = 9 escolas.
Questão 2
A Câmara de Vereadores de um município é composta por 16 mulheres e 12 homens, que serão divididos no maior número possível de comissões de tal forma que cada comissão tenha o mesmo número de membros. O número de membros em cada comissão é igual a:
A) 8.
B) 7.
C) 6.
D) 5.
E) 4.
Resolução:
Alternativa E.
Encontrando o MDC entre 16 e 12, temos que:
D(16) = {1, 2, 4, 8, 16}
D(12) = {1, 2, 3, 4, 6, 12}
Analisando as listas, o maior divisor em comum entre esses números é 4.
MDC(16, 12) = 4
Então, cada comissão terá um total de 4 pessoas.





