Números pares e ímpares

Números pares e ímpares são caracterizações dos números inteiros. Chamamos um número inteiro de par caso ele seja divisível por 2 e de ímpar caso ele não seja divisível por 2. O último algarismo dos números pares é 0, 2, 4, 6 ou 8; já dos números ímpares é 1, 3, 5, 7 ou 9.

Leia também: O que são múltiplos e divisores de um número?

Tópicos deste artigo

• 1 - O que são números pares?
• 2 - O que são números ímpares?
  • → Propriedades dos números ímpares
• 3 - Quais são os números pares e ímpares de 1 a 100?
• 4 - Exercícios resolvidos sobre números pares e ímpares

O que são números pares?

Um número inteiro é par se ele é divisível por 2, ou seja, se a divisão desse número por 2 tem resto igual a 0.

Consequentemente, todos os múltiplos de 2 são pares. Assim, todo número par pode ser escrito na forma , em que é um número inteiro.

Isso significa que um número inteiro é par se o algarismo da ordem das unidades é 0, 2, 4, 6 ou 8.

Exemplo 1:

Explique por que o número 32 é par.

Resolução:

Podemos ver isso de três formas:

• Perceba que dividindo 32 por 2 obtemos 16 como quociente e 0 como resto. Portanto, 32 é um número par.

• Podemos também visualizar o número 32 como a multiplicação entre os números 2 e 16. Assim, 32 é múltiplo de 2 e, portanto, é um número par.

• Observe que o número 32 possui o algarismo 2 na ordem das unidades. Logo, 32 é par.

Exemplo 2:

Verifique se o número 10.634 é par ou não.

Resolução:

Perceba que o algarismo na ordem das unidades (o último algarismo) é 4. Logo, esse número é par.

→ Propriedades dos números pares

Propriedades são características em comum a certos elementos. Assim, vejamos algumas propriedades relacionadas à soma e produto entre números pares.

◦ A soma de dois números pares resulta em um número par

O número 38 é par, e o número 66 também é par. A soma desses números é igual a 104, que também é um número par, pois o algarismo das unidades é 4.

◦ O produto de dois números pares resulta em um número par

O número 12 é par, e o número 8 também é par. O produto desses números é 96, que também é um número par, pois o algarismo das unidades é 6.

O que são números ímpares?

Um número inteiro é ímpar se ele não é divisível por 2, ou seja, se a divisão desse número por 2 tem resto igual a 1.

Consequentemente, um número é ímpar se ele for um múltiplo de 2 acrescido de uma unidade. Assim, todo número ímpar pode ser escrito na forma , em que é um número inteiro.

Isso significa que um número inteiro é ímpar se o algarismo da ordem das unidades é 1, 3, 5, 7 ou 9.

Exemplo 1:

Explique por que o número 27 é ímpar.

Resolução:

Podemos explicar isso de três maneiras:

• Perceba que dividindo 27 por 2 obtemos 13 como quociente e 1 como resto. Portanto, 27 é um número ímpar.

• Observe que podemos visualizar o número 27 como a multiplicação entre os números 2 e 13 acrescida de 1 (), portanto 27 não é múltiplo de 2, sendo assim um número ímpar.

• Por fim, perceba que 27 é ímpar, pois possui o algarismo 7 na ordem das unidades.

Exemplo 2:

Verifique se o número 304.761 é ímpar ou não.

Resolução:

Note que o algarismo na ordem das unidades (o último algarismo) é 1. Logo, esse número é ímpar.

Importante: Concluímos que cada número inteiro é, necessariamente, classificado como par ou ímpar.

→ Propriedades dos números ímpares

Vejamos algumas propriedades relacionadas à soma e produto entre números ímpares e também entre números pares e ímpares.

◦ A soma de dois números ímpares resulta em um número par

Os números 47 e 53 são ímpares. Sua soma é igual a 100, que é um número par, pois o algarismo das unidades é 0.

◦ O produto de dois números ímpares resulta em um número ímpar

Os números 13 e 7 são ímpares. Seu produto é 91, que é um número ímpar, pois o algarismo das unidades é 1.

◦ A soma de um número par por um número ímpar resulta em um número ímpar

O número 24 é par, e o número 31 é ímpar. Sua soma é 55, que é um número ímpar, pois o algarismo das unidades é 5.

◦ O produto de um número par por um número ímpar resulta em um número par

O número 14 é par, e o número 3 é ímpar. Seu produto é 42, que é um número par, pois o algarismo das unidades é 2.

Quais são os números pares e ímpares de 1 a 100?

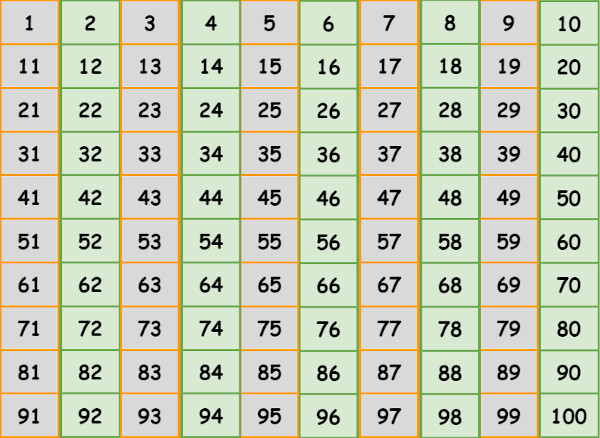
Lembre-se que os números pares possuem 0, 2, 4, 6 ou 8 como algarismo da ordem das unidades enquanto os números ímpares possuem 1, 3, 5, 7 ou 9 como algarismo da ordem das unidades.

Levando isso em conta, reunimos abaixo todos os números pares (destacados em verde) e todos os números ímpares (destacados em cinza) de 1 a 100.

Saiba mais: Números complexos — o conjunto de números formados por uma parte real e uma parte imaginária

Exercícios resolvidos sobre números pares e ímpares

Questão 1

Três amigos decidiram se reunir depois da aula de Matemática para estudar um pouco mais sobre números pares e ímpares. Assim, cada um fez afirmações sobre as propriedades de soma e produto entre números pares e ímpares:

• Alan: A soma entre dois números pares resulta em um número par, e o produto de dois números ímpares resulta em um número par.

• Beatriz: A soma de entre dois números ímpares resulta em um número par, e o produto entre um ímpar e um par resulta em um número par.

• Camila: A soma entre um número par e um ímpar resulta em um número ímpar, e o produto de dois números pares resulta em um número par.

Entre os amigos, aqueles que fizeram apenas afirmações corretas foram:

A) Alan e Beatriz.

B) Alan e Camila.

C) Beatriz e Camila.

D) Nenhum dos três amigos.

Resolução:

Alternativa C

Perceba que o único que fez uma afirmação equivocada foi Alan, pois o produto entre dois números ímpares resulta em um número ímpar.

Questão 2

(Unicamp) Considere três números inteiros cuja soma é um número ímpar. Entre esses três números, a quantidade de números ímpares é igual a:

A) 0 ou 1.

B) 1 ou 2.

C) 2 ou 3.

D) 1 ou 3.

Resolução:

Alternativa D

Vejamos as possibilidades de soma de três números que resultam em um número par ou ímpar:

• Se um deles for par e o resto for ímpar: par + ímpar + ímpar = par

• Se um deles for ímpar e o resto for par: par + par + ímpar = ímpar

• Se todos forem pares: par + par + par = par

• Se todos forem ímpares: ímpar + ímpar + ímpar = ímpar

Assim, a soma de três números inteiros será ímpar se apenas um desses números for ímpar ou se todos os três números forem ímpares.

Maria Luiza Alves Rizzo
Professora de Matemática