Ao estudar o conjunto dos Números Racionais, encontramos algumas frações que, ao serem convertidas em números decimais, tornam-se dízimas periódicas. Para realizar essa transformação, devemos dividir o numerador da fração pelo seu denominador, como no caso da fração 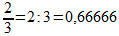 . Do mesmo modo, através de uma dízima periódica, podemos encontrar a fração que lhe deu origem. Essa fração é chamada de “Fração Geratriz”.
. Do mesmo modo, através de uma dízima periódica, podemos encontrar a fração que lhe deu origem. Essa fração é chamada de “Fração Geratriz”.
Em qualquer dízima periódica, o número que se repete é chamado de período. No exemplo dado, temos uma dízima periódica simples, e o período é o número 6. Através de uma equação simples, podemos encontrar a fração geratriz de 0,6666…
Primeiramente, podemos afirmar que:
x = 0,666...
A partir daí, verificamos quantos algarismos possui o período. Nesse caso, o período possui um algarismo. Vamos então multiplicar ambos os lados da equação por 10, caso o período tivesse 2 algarismos, multiplicaríamos por 100, no caso de 3 algarismos, por 1000, e assim sucessivamente. Então, teremos:
10x = 6,666...
No segundo membro da equação, podemos desmembrar o número 6,666… em um número inteiro e em outro decimal da seguinte forma:
10 x = 6 + 0,666...
Todavia, logo no início afirmamos que x = 0,666..., então podemos substituir a parte decimal na equação por x e ficaremos com:
10 x = 6 + x
Utilizando as propriedades básicas de equações, podemos então mudar a variável x do segundo para o primeiro lado da equação:
10 x - x = 6
Resolvendo a equação, teremos:
9 x = 6
x = 6
9
Simplificando a fração por 3, temos:
x = 2
3
Logo, 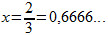 , ou seja,
, ou seja, 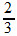 é a fração geratriz da dízima periódica 0,6666... .
é a fração geratriz da dízima periódica 0,6666... .
Vejamos quando temos uma dízima periódica composta, como no caso de 0,03131… Iniciaremos do mesmo modo:
x = 0,03131...
A fim de deixar essa igualdade mais semelhante com a do exemplo anterior, precisamos alterá-la para que não tenhamos nenhum número entre o sinal de igualdade e o período. Para isso, vamos multiplicar a equação por 10:
10 x = 0,313131... ***
Seguindo o raciocínio utilizado no primeiro exemplo, temos que a dízima periódica possui período com dois algarismos, vamos então multiplicar a equação por 100.
1000 x = 31,313131...
Agora basta desmembrar a parte inteira da decimal, no segundo membro da igualdade.
1000 x = 31 + 0,313131...
Mas por ***, temos que 10 x = 0,313131..., vamos então substituir o número decimal por 10 x.
1000 x = 31 + 10 x
1000 x - 10 x = 31
990 x = 31
x = 31
990
Então, a fração geratriz de 0,0313131… é 31 . Essa regra pode ser aplicada para todas as dízimas periódicas.
990
Por Amanda Gonçalves
Graduada em Matemática




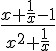 é:
é: