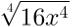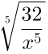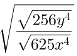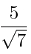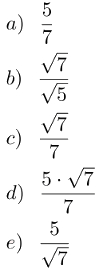Certas situações envolvendo radicais podem ser simplificadas utilizando algumas técnicas matemáticas. Vamos, através de propriedades, demonstrar como simplificar números na forma de radicais, isto é, números ou letras que podem possuir raízes exatas ou não. Nesse último caso, a simplificação é primordial para os cálculos futuros.
.jpg "Raiz enésima")
Elementos de um radical, raiz enésima de um número
n = índice da raiz
x = radicando
y = expoente do radicando
Propriedades dos radicais:
1º propriedade: O expoente do radicando é menor que o índice. Dessa forma, reduzimos o índice e o expoente através da utilização do máximo divisor comum aos termos. Observe:
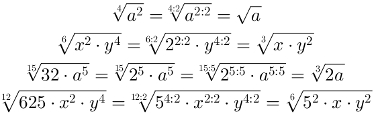
2ª propriedade: O expoente do radicando é maior ou igual ao índice. Dessa forma, simplificamos o expoente pelo mesmo valor do índice e retiramos a base do radicando.
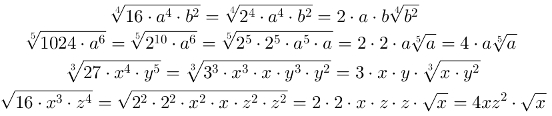
3ª propriedade: Introdução de termos no radicando. O termo externo introduzido no radicando recebe como expoente o mesmo valor numérico do índice.
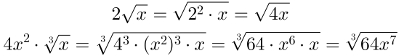
4ª propriedade: Simplificação de radicais com frações algébricas no radicando.
5ª propriedade: Raiz de números na forma de fração. Nesse caso, devemos extrair a raiz do numerador e do denominador da fração numérica, fornecendo o resultado na forma de fração.
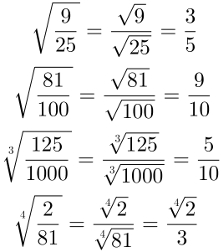
6ª propriedade: Racionalização de denominadores. Pode ocorrer em algumas frações a presença de radicais no denominador. Caso a raiz do radical envolva como resultado números irracionais, o cálculo se torna complexo. Por isso, devemos racionalizar as frações com radicais no denominador. A racionalização é feita multiplicando os membros da fração pelo radical presente no denominador. Observe os exemplos:
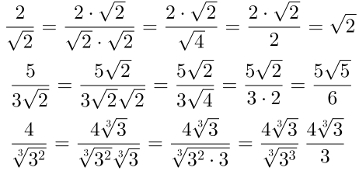
Por Marcos Noé
Graduado em Matemática
Gostaria de fazer a referência deste texto em um trabalho escolar ou acadêmico? Veja:
SILVA, Marcos Noé Pedro da. "Simplificação de radicais"; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/simplificacao-radicais.htm. Acesso em 20 de junho de 2021.
Qual das alternativas a seguir é a simplificação do seguinte radical?
a) x
b) 2x
c) 3x
d) 4x
e) 16x
Qual das alternativas a seguir é resultado da simplificação do radical a seguir?
a) 1/x
b) 2/x
c) 3/x
d) 4/x
e) √32
x
