A raiz quadrada é uma operação matemática que acompanha todos os níveis escolares. Trata-se de um caso particular de radiciação, no qual o índice do radical é igual a 2, ou seja, é a operação inversa das potências de expoente igual a 2. Quando um número positivo possui raiz quadrada exata, dizemos que esse número é um quadrado perfeito.
Leia também: Propriedades envolvendo números complexos
Tópicos deste artigo
- 1 - Definição e nomenclatura dos elementos da radiciação
- 2 - Como calcular uma raiz quadrada?
- 3 - Observações:
- 4 - Mapa Mental: Raiz Quadrada
- 5 - Interpretação geométrica da raiz quadrada
- 6 - Exercícios resolvidos
Definição e nomenclatura dos elementos da radiciação
Sejam a e b dois números reais e n um número natural diferente de zero, então:
![]()
a = radicando
n = índice
√ = radical
As raízes quadradas, como dito, são um caso particular de radiciação. Ao escrever uma raiz quadrada, não é necessário explicitar o índice igual a dois.
![]()
Para os demais tipos de raízes, é obrigatório colocar o índice, ou seja, para n = 3, n = 4, n = 5 …, é necessário deixar explícito no índice do radical o valor de n.
Leia também: Redução de radicais ao mesmo índice
Como calcular uma raiz quadrada?
Para calcular a raiz quadrada de um número real, basta seguir a definição de radiciação:
![]()
A definição nos diz que a raiz quadrada de um número real a é o número b se, e somente se, o número b elevado ao quadrado for igual ao número a, ou seja, temos que imaginar um número que, ao quadrado, resulte no número dentro do radical.
Exemplos:
√36 = 6, pois 62 = 36
√121 = 11, pois 112 = 121
Os números que possuem raiz quadrada são denominados quadrados perfeitos. Assim, dos exemplos acima, os números 36 e 121 são quadrados perfeitos. Quando o número não é um quadrado perfeito, é necessário realizar o cálculo de raízes não exatas.

Observações:
1. Perceba, com base na definição de raiz quadrada, que sempre procuramos um número que, quando elevado ao quadrado, resulta no número dentro do radical. Tendo em vista as propriedades da potenciação, sabemos que um número ao quadrado é sempre positivo. Isso nos leva a concluir que não é possível extrair raiz quadrada de um número negativo no conjunto dos números reais.
Exemplo:
√ — 36 = ?
Do exemplo acima, teríamos que imaginar um número que, elevado ao quadrado, resultaria em -36. No conjunto dos números reais, isso não é impossível.
2. Caso o radicando seja um número relativamente grande, o que impossibilitaria o cálculo mental, basta fazer a decomposição em primos e agrupar sempre que possível em potências de expoente dois.
Exemplo:
Vamos determinar o valor da raiz quadrada de 441.
√441
Para determinar a raiz de 441, vamos fazer a decomposição em primos:
441 = 32 . 72
Assim,
√441 = √32 . 72
Agora, aplicando as propriedades de radiciação, temos que:
√441 = 3 . 7 = 21
O número 21 elevado ao quadrado é igual a 441.
Mapa Mental: Raiz Quadrada
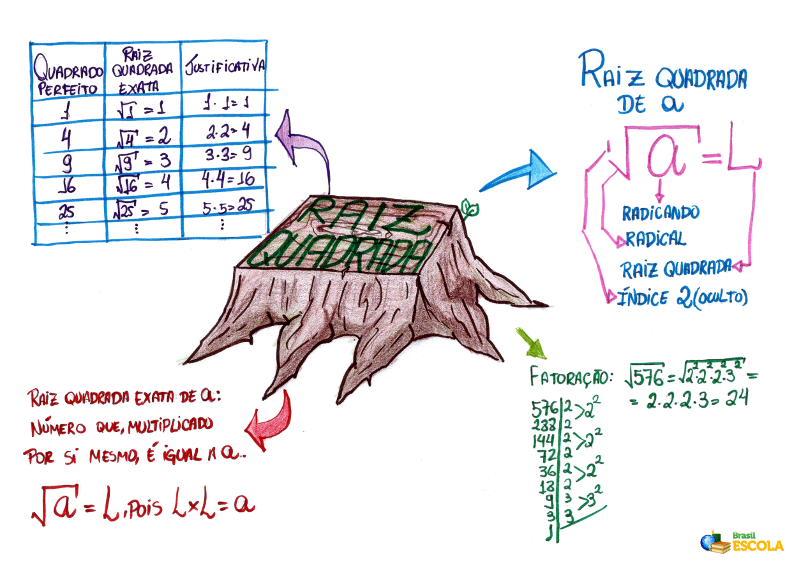
*Baixe o mapa mental sobre raiz quadrada!
Interpretação geométrica da raiz quadrada
Imagine um terreno com área de 144 m2.

Para determinar quanto mede o lado desse terreno em forma de quadrado, temos que relembrar como calcular sua área.
Aquadrado = l2
A representa o valor da área, e l é o valor do lado.
Como a área vale 144 m2, temos que:
144= l2
Observe a equação acima. Note que precisamos encontrar um número que, elevado ao quadrado, seja igual a 144, isto é, temos a definição de raiz quadrada! Então:
√144 = 12
O número 144 na forma fatorada é:
144 = 22 . 22 . 32
Assim, vamos ter que:
√144 = √22 . 22 . 32
Por fim,
√144 = 2 . 2 . 3 = 12
Portanto, o lado do terreno mede 12 m.
Exercícios resolvidos
1. Elabore uma lista com os quadrados perfeitos de 1 a 100.
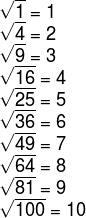
Os quadrados perfeitos de 1 a 100 são: 1, 4, 9, 16, 25, 36, 49, 64, 81 e 100
2. Determine a raiz quadrada do número 1024.
√1024
Para determinar a raiz de 1024, vamos fazer a decomposição em primos:
1024 = 22 . 22 . 22 . 22 . 22
Então,
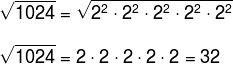
Considerando a segunda igualdade com as propriedades da radiciação já aplicadas.
*Mapa Mental por Luiz Paulo Silva
Graduado em Matemática


