Como reconhecer os números primos

Os números primos fazem parte do sistema de numeração cardinal, que é composto pelos números naturais 0, 1, 2, 3, 4... A descoberta dos números primos ocorreu em Alexandria, por volta de 360 a.C a 295 a.C, pelo estudioso Euclides. Foi ele quem descobriu que existe uma quantidade infinita de números primos e que qualquer número composto pode ser decomposto em fatores primos. Lembre-se que número composto é todo número natural maior que um e que possui como divisor mais de dois números naturais. São números compostos: 4, 6. 8, 9, 10, 12. . .

A forma mais conhecida para identificar números primos é o Crivo de Eratóstenes, que é um algoritmo prático utilizado em intervalos numéricos. Eratóstenes era da Grécia e viveu no período de 276 a.C a 194 a.C, foi um grande matemático e ficou conhecido por ter calculado a circunferência da Terra.

São considerados números primos os termos numéricos maiores que 1, divisíveis por 1 e por ele mesmo. O número 1 não é primo, sendo assim, os números primos são: 2, 3, 7, 11, 13, 17, 19, 23, 29, 31 . . .

Mas, como reconhecer os números primos?

Para identificar um número primo devemos dividi-lo sucessivamente por números primos como: 2, 3, 5. . . e verificar se a divisão é exata (em que o resto é zero) ou não exata (onde o resto é diferente de zero).

• Se o resto da divisão for zero o número não é primo.

• Se nenhum resto for zero, o número é primo.

Para dividir um número de forma mais rápida podemos utilizar os critérios de divisibilidade, mas somente quando os divisores forem números primos, como 2, 3, 5 e 11. Recorde-se que:

• Um número é divisível por 2 quando terminado em termos pares, ou seja, 0, 2, 4, 6. . .

• Um número será divisível por três quando a soma dos seus algarismos for divisível por 3.

• Um número será divisível por 5 quando o seu último algarismo for 5 ou 0.

Um número será divisível por 11 quando a diferença da soma dos algarismos de ordem par com a soma dos algarismos de ordem ímpar obtiver como resultado um número divisível por 11.

Ao falarmos de resto, devemos sempre nos lembrar do algoritmo da divisão, que é dado por:

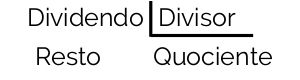
Veja o exemplo a seguir:

Descubra se o número 521 é primo.

Para descobrirmos se o número 521 é primo devemos verificar quais os divisores de 521. Podemos fazer isso utilizando os critérios de divisibilidade, ou seja, dividindo 521 pelos números primos: 2, 3, 5. Iremos parar de dividir 521 por números primos quando o valor do quociente for menor que o do divisor. Caso nenhum resto das divisões seja igual a zero, o número será considerado primo.

• De acordo com o critério de divisibilidade, o 521 não é divisível por dois, porque não é um número par.

• 521 não é divisível por 3, porque a soma dos algarismos que o compõe não é divisível por 3. Veja 5 + 1 +1 = 7

• O número 521 também não é divisível por 5, porque o último algarismo do número 521 não é 5.

• 521 não é divisível por 7, já que sete é uma divisão não exata e seu resto é 3.

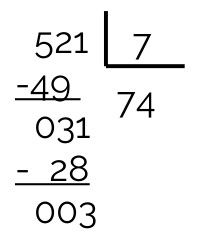
• O número 11 também não é divisor de 521, porque o seu resto é 4. Observe que o quociente é maior que o divisor, sendo assim, devemos dividir 521 pelo próximo número primo, que é 13.

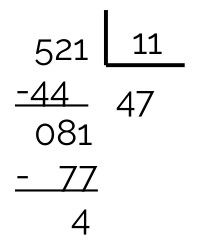
• 521 não é divisível por 13, porque a sua divisão não é exata.

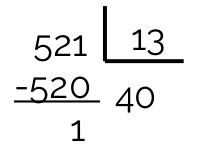
• 17 não é divisor de 521, pois o resto da divisão é 11. Com isso teremos que dividir pelo próximo número primo, que é 19.

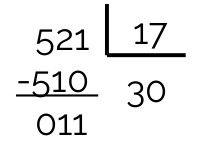
• 521 não é divisível por 19, porque o resto dessa divisão é 8.

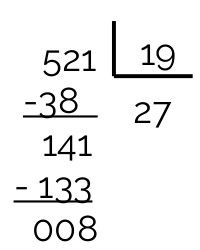
• 23 não é divisor de 521, o resto da divisão é 15. Como o quociente (22) é menor que o divisor (23), devemos parar de dividir o número 521.

Concluímos que 521 é um número primo, sendo assim, é divisível somente por 1 e por ele mesmo (521).

Por Naysa Oliveira
Graduada em Matemática