Números Triangulares

Imagine-se em uma brincadeira com bolinhas de gude para a formação de triângulos. Você pode considerar primeiramente que uma bolinha é como um pequeno triângulo:

•

Em seguida, você coloca duas bolinhas abaixo e forma os três vértices de um triângulo:

•
• •

Se você colocar outras três bolinhas abaixo dessas, formará outro triângulo:

•
• •
• • •

A cada etapa de acréscimo de bolinhas em relação à quantidade colocada anteriormente, haverá sempre a formação de triângulos. Veja o triângulo formado com a adição de mais quatro bolinhas:

•
• •
• • •
• • • •

A quantidade total de bolinhas em cada etapa caracteriza uma classe de números chamada de números triangulares. O matemático Karl Friedrich Gauss descobriu uma fórmula para indicar a quantidade total em cada triângulo, em que S₁ correspondia ao primeiro triângulo, S₂, ao segundo triângulo, e assim sucessivamente. As somas descritas por Gauss iniciavam com um e, a cada etapa, era adicionado um número que correspondia a uma unidade acima do último número adicionado:

S₁ = 1
​S₂ = 1 + 2 = 3
S₃ = 1 + 2 + 3 = 6
S₄ = 1 + 2 + 3 + 4 = 10
S₅ = 1 + 2 + 3 + 4 + 5 = 15

Os resultados dessas somas foram os números triangulares: 1, 3, 6, 10, 15... Observe que existe um padrão estabelecido em cada uma dessas somas. Analisando cuidadosamente, podemos observar que cada uma delas é uma progressão aritmética de razão 1. Então vale aqui a soma de Gauss, que estabelece que, em uma soma de razão constante, se adicionarmos o primeiro elemento ao último, obteremos o mesmo resultado de somarmos o segundo elemento ao penúltimo. Vejamos como ocorre o processo da soma de Gauss para as somas S₆ e S₇:

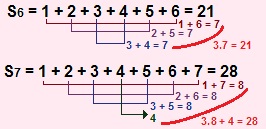
Processo da soma de Gauss aplicado à soma dos números triangulares

Se para S₆ e S₇ temos as somas da imagem acima, vamos reproduzir essa soma para S₈, S₉, S₁₀ e S₁₁:

S₈ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 4.9 = 36
S₉ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4.10 + 5 = 45
S₁₀ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 5.11 = 55
S₁₁ = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11= 5.12 + 6 = 66

Podemos generalizar para obter uma soma para S_n:

S_n = n. (n + 1), se n é par
2         

S_n = (n - 1).(n + 1) + (n - 1) + 1, se n é ímpar
​2                      2                    

Assim como na magia dos números, podemos mostrar outro fato interessante acerca dos números triangulares: a soma de números triangulares subsequentes resulta sempre em números que podem ser classificados como quadrados perfeitos, isto é, números que possuem raiz quadrada. Vejamos:

S₁ + S₂ = 1 + 3 = 4
​S₂ + S₃ = 3 + 6 = 9
S₃ + S₄ = 6 + 10 = 16
S₄ + S₅ = 10 + 15 = 25
S₅ + S₆ = 15 + 21 = 36
S₆ + S₇ = 21 + 28 = 49
S₇ + S₈ = 28 + 36 = 64
​S₈ + S₉ = 36 + 45 = 81
S₉ + S₁₀ = 45 + 55 = 100
S₁₀ + S₁₁ = 55 + 66 = 121

Os resultados obtidos, 4, 9, 16, 25, 36, 49, 64, 81, 100 e 121, são todos quadrados perfeitos.

Por Amanda Gonçalves
Graduada em Matemática