Matemática financeira

A matemática financeira é uma das áreas da matemática responsável por estudar fenômenos relacionados ao mundo financeiro. Além disso, estudar seus conceitos faz-se muito importante, uma vez que, em nosso cotidiano, eles estão cada vez mais presentes, por exemplo, ao recebermos um desconto ao comprar algo à vista ou um acréscimo ao comprar algo parcelado.

 Estudar matemática financeira requer um conhecimento prévio sobre porcentagem, veremos que todos os conceitos são baseados nesse tema. 

Leia também: Cálculo de porcentagem com regra de três

Tópicos deste artigo

• 1 - Para que serve a matemática financeira?
• 2 - Conceitos básicos da matemática financeira
  • Acréscimo
  • Desconto
  • Juros simples
  • Juros compostos
• 3 - Exercícios resolvidos

Para que serve a matemática financeira?

A matemática financeira é utilizada diariamente, por exemplo, quando vamos realizar uma compra à vista e o vendedor oferece um desconto de 5% no valor do produto, ou quando optamos em realizar a compra de um produto em parcelas e, nesse processo, uma taxa de juros é cobrada do comprador ao decorrer do tempo.

Um exemplo da importância de entender-se os conceitos da matemática financeira é o chamado limite de cheque especial. Ao abrir-se uma conta em determinado banco, é oferecido um dinheiro “extra”, para emergências, por exemplo. Entretanto, ao usar-se esse limite ou parte dele, é cobrada, além do dinheiro pego, uma taxa a ser paga posteriormente. Essa taxa é chamada de juros, e, compreendendo melhor esses conceitos, podemos traçar uma melhor estratégia de administração das finanças.

• Exemplo 1

Uma pessoa está precisando de 100 reais para terminar de pagar suas contas mensais, entretanto todo seu salário já foi gasto com as demais contas. Em analise, essa pessoa verificou que dispunha de duas opções.

Opção 1 – Usar o limite do cheque especial oferecido pelo banco, sob uma taxa de 0,2% ao dia, para ser pago em um mês.

Opção 2 – Pegar com um amigo os 100 reais, sob uma taxa de 2% ao mês, para serem pagos durante dois meses.

Utilizando-nos apenas do conhecimento de porcentagem, vamos analisar qual a melhor opção.

Analisando a opção 1, observe que a taxa de 0,2% é cobrada por dia, ou seja, a cada dia é acrescentado 0,2% do valor do empréstimo, assim:

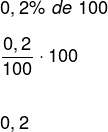
Como o empréstimo deve ser pago em um mês, e considerando-se o mês com 30 dias, o valor a ser pago de juros é de:

0,2 · 30

6

Dessa forma, podemos concluir que o valor a ser pago no fim de um mês é de:

100 + 6 = 106 reais

100 → Valor emprestado pelo banco

6 → Valor do juros

Agora analisando-se a opção 2, a taxa cobrada é de 2% ao mês e deve ser paga no período de dois meses, ou seja, a cada mês, 2% do valor emprestado é acrescido à dívida, assim:

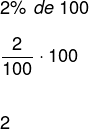
Observe que deve ser acrescido, no valor da dívida, 2 reais por mês:

2 · 2 = 4

Portanto, o valor a ser pago no final do período é de:

100 + 4 = 104 reais

100 → Valor emprestado pelo amigo

4 → Valor do juros

Assim, podemos concluir que a melhor opção é pegar o dinheiro com o amigo. Essa é uma simples e importante aplicação da matemática financeira, claro que existem problemas, ferramentas e conceitos mais sofisticados, mas, como tudo na vida, antes de compreender-se a parte complexa, é necessário entender-se o básico.

Conceitos básicos da matemática financeira

Os principais conceitos da matemática financeira envolvem o conhecimento prévio sobre porcentagem. Veremos, a seguir, conceitos como acréscimo, desconto, juros simples e juros compostos.

• Acréscimo

A ideia do acréscimo está associada a adicionar ou acrescentar parte do valor a seu valor original, ou seja, adicionamos uma porcentagem de determinado valor nele mesmo. Veja o exemplo:

• Exemplo 2

Um produto custava 35 reais, com o aumento do dólar, ele sofreu um acréscimo de 30%. Determine o novo valor desse produto.

Muitas vezes, quando vamos fazer as contas relacionadas a acréscimo, elas são executadas de maneira errada escrevendo-se:

35 + 30%

A porcentagem representa parte de algo, assim, para essa conta ficar correta, devemos calcular primeiro 30% do valor inicial, nesse caso, 35. Assim:

35 + 30% de 35

Resolvendo primeiro a porcentagem e, em seguida, somando os valores, teremos que:

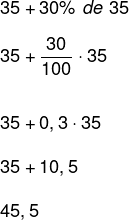
Portanto, com o acréscimo, o valor no produto será de 45,5 reais (quarenta e cinco reais e cinquenta centavos).

De modo geral, podemos deduzir uma fórmula para o acréscimo. Considere um valor x e que ele sofra um acréscimo de p%. De acordo com o que acabamos de definir, podemos escrever esse acréscimo da seguinte maneira:

x + p% de x

Desenvolvendo essa expressão, teremos que:

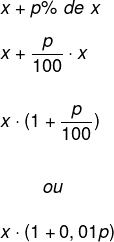
Vamos refazer o exemplo 2 utilizando a fórmula anterior. Observe que x = 35 e que o acréscimo foi de 30%, ou seja, p = 30%.

35 · (1 + 0,01 · 30)

35 · (1 + 0,3)

35 · 1,3

45,5

Observe que foi obtido o mesmo valor, e é uma opção utilizar tal fórmula.

Veja também: Grandezas inversamente proporcionais

• Desconto

A ideia de desconto é similar à ideia de acréscimo, a única diferença é que, em vez de adicionar, devemos subtrair uma porcentagem do valor original.

• Exemplo 3 – Um produto que custa 60 reais, quando comprado à vista, possui um desconto de 30%. Determine o novo valor desse produto.

De maneira similar ao acréscimo, teremos que:

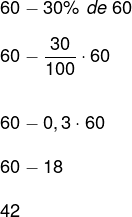
De modo análogo ao acréscimo, podemos deduzir uma fórmula para o desconto. Considere um valor x e que ele sofra um desconto de p%. De acordo com que definimos, podemos escrever esse acréscimo da seguinte maneira:

x – p% de x

Desenvolvendo essa expressão, teremos que:

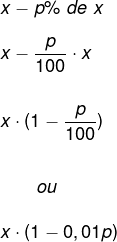
Vamos refazer o exemplo 3 utilizando a fórmula anterior, observe que x = 60 e que o acréscimo foi de 30%, ou seja, p = 30%.

x · (1 – 0,01p)

60 · (1 – 0,01 · 30)

60 · (1 – 0,3)

60 · 0,7

42

Veja que, utilizando a fórmula, obtivemos o mesmo resultado, assim, no desconto também temos duas opções para determiná-lo.

• Juros simples

A ideia por trás do juros simples também é similar à ideia do acréscimo, a diferença entre eles é dada pelo período em que são calculados. Enquanto a taxa do acréscimo é aplicada uma vez, a do juros simples é calculada em um intervalo de tempo. Podemos calcular o juros simples de determinado capital C, aplicado à determinada taxa a regime de juros simples (i), em um determinado período de tempo t, pela fórmula:

J = C · i · t

O valor pago ao final dessa aplicação deve ser dado pelo dinheiro aplicado mais o valor do juros e recebe o nome de montante (M). O montante é dado pela expressão:

M = C + J

M = C + C · i · t

M = C (1 + it)

A única preocupação que devemos ter em relação a problemas envolvendo juros simples é com as unidades de medida de taxa e tempo, elas devem sempre estar em unidades iguais.

• Exemplo 4

Marta deseja aplicar R$ 6000 em uma empresa que promete gerar lucros de 20% ao ano sob regime de juros simples. O contrato feito por Marta afirma que ela só pode tirar o dinheiro após seis meses, determine qual foi o rendimento de seu dinheiro no final desse período.

Observando o enunciado, veja que o capital é igual a 6000, logo, temos que C = 6000. A taxa de juros é de 20% ao ano, e o dinheiro ficará aplicado durante seis meses. Observe que a taxa foi dada ao ano, e a do tempo, em meses, e sabemos que a unidade de medida de ambas devem ser a mesma. Vamos encontrar o valor mensal da taxa, veja:

Sabemos que a taxa é de 20% ao ano, como um ano tem 12 meses, logo, a taxa mensal será de:

20% : 12

1,66% ao mês

0,016 ao mês

Substituindo esses dados na fórmula, temos que:

J = C · i · t

J = 6000 · 0,016 · 6

J = 96 · 6

J = 576 reais

Portando, o valor a ser retirado no fim dos seis meses é de 576 reais, e o montante é de:

M = 6000 + 576

M = 6576 reais

Leia mais: Noções sobre utilização de uma calculadora financeira

• Juros compostos

No juros simples, o valor da taxa de juros é sempre calculado em cima do capital inicial, a diferença entre esses dois sistemas (juros simples e compostos) está justamente nesse ponto, ou seja, na forma como a taxa é calculada. No juros composto, a taxa de juros é sempre calculada em cima do capital do mês anterior, isso faz com que o juros aumente de maneira exponencial seu valor. A fórmula para calcular-se o juros no sistema de amortização de juros compostos é dada por:

M = C · (1 + i)^t

Em que M é o montante acumulado, C é o valor do capital inicial, i é a taxa de juros dada em porcentagem, e t é o período no qual o capital ficou aplicado no sistema. Da mesma forma que no juros simples, no sistema de juros compostos, a taxa e o tempo devem ficar na mesma unidade.

• Exemplo 5

Calcule o valor do montante que Marta recolheria no final dos seis meses ao aplicar seus 6000 reais sob taxa de juros de 20% ao ano no regime de juros compostos.

(Dado: 1,2^0,5 ≈ 1,095)

Observe que os dados são os mesmos do exemplo 4, logo, temos que:

C = 6000

i = 0,2 a.a

t = 0,5 anos

Substituindo os dados na fórmula de juros compostos, temos que:

M = 6000 · (1 + 0,2)^0,5

M = 6000 · (1,2)^0,5

M = 6000 · 1,095

M = 6572,67 reais

Portanto, o montante a ser retirado por Marta no sistema de juros simples é de 6572, 67 reais. Veja que o montante no sistema de juros compostos é maior que no de juros simples, e isso ocorre em todos os casos. Para compreender melhor como é o cálculo dessa taxa, acesse: Juros compostos.

Exercícios resolvidos

Questão 1 – (FGV – SP) Um capital aplicado a juros simples, à taxa de 2,5% ao mês, triplica em:

a) 75 meses

b) 80 meses

c) 85 meses

d) 90 meses

e) 95 meses

Resolução

Alternativa B.

Devemos encontrar o tempo em que o juros seja igual a 2C, uma vez que, com o juros dessa forma junto ao capital aplicado inicialmente de C, teremos o montante de 3C (triplo do capital). Assim:

J = 2C; C = C; i = 2,5% ao mês; t = ?

J = C · i · t

2C = C · 0,025 · t

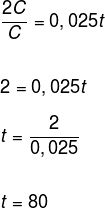
Assim, o tempo para que esse capital triplique é de 80 meses.

Observação: 80 meses equivale a 6,6 anos.

Questão 2 – Uma mercadoria, após sofrer um amento de 24%, teve seu preço alterado para 1041,60 reais. Determine o valor antes do acréscimo.

Resolução

Podemos utilizar a fórmula geral do acréscimo para determinar o valor da mercadoria antes do acréscimo.

x · (1 + 0,01p)

Na fórmula, o valor x é o que buscamos e p é o valor do acréscimo, e essa expressão fornece-nos o valor do produto após o acréscimo, logo:

1041,60 = x · (1 + 0,01p)

1041,60 = x · (1 + 0,01 · 24)

1041,60 = x · (1 + 0,24)

1041,60 = x · 1,24

Veja que temos uma equação do primeiro grau, para resolvê-la, devemos isolar a incógnita x, dividindo ambos lados da igualdade por 1,24, ou, simplesmente, passar o 1,24 dividindo. Assim:

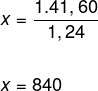
Portanto, o valor da mercadoria antes do acréscimo era de 840 reais.

 

Por Robson Luiz
Professor de Matemática