A razão entre dois números é dada pela sua divisão obedecendo a ordem na qual eles foram dados. Tal razão pode ser representada na forma fracionária, decimal e percentual. A relação entre duas ou mais razões é uma importante ferramenta para solucionar problemas práticos, essa igualdade é chamada de proporção.
Leia também: Propriedades da proporção: quais são e para que servem?
Tópicos deste artigo
Razão e proporção
→ Definição de razão: Considere dois números racionais x e y, com y diferente de zero. A razão de x por y, nessa ordem, é dada pelo quociente:
![]()
-
Exemplo
A razão entre os números:
a) 3 e 4
b) 5 e 7
Devemos ficar bastante atentos à ordem na qual os números são dados, o primeiro número sempre será o numerador, e o segundo número sempre será o denominador. Veja:
![]()
→ Definição de proporção: Quando igualamos duas razões, estamos formando uma proporção. Considere duas razões em que b ≠ 0 e y ≠ 0:
![]()
A igualdade será uma proporção se a · y = b · x, ou seja, se multiplicando cruzado encontrarmos uma igualdade verdadeira, então teremos uma proporção
-
Exemplo
Verificar se os números 2, 3, 10 e 15 são proporcionais nessa ordem.
Para isso, devemos montar a razão entre esses números e, em seguida, multiplicar cruzado. Se encontrarmos uma igualdade verdadeira, então eles serão proporcionais, caso contrário, eles não serão proporcionais.
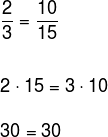
Veja também: Proporcionalidade entre grandezas: tipos e exemplos
Como representar uma razão?
Vimos que uma razão é dada por uma divisão, que, por sua vez, pode ser representada por uma fração. Ao realizar a divisão do numerador pelo denominador dessa fração, obteremos a forma decimal da razão. Com base na forma decimal, podemos escrever a razão em sua forma percentual, bastando multiplicar esse número decimal por 100. Veja os exemplos.
-
Exemplo
Representação da razão entre 2 e 4 na forma fracionária, decimal e percentual.
A razão entre 2 e 4 é dada por:
![]()
Para determinar a forma decimal, basta realizar a divisão do numerador pelo denominador.
2 ÷ 4 = 0,5
Portanto, 0,5 é a representação decimal da razão dos números 2 e 4.
Para escrevermos essa razão na forma percentual, devemos multiplicar por 100 o número 0,5. Veja:
0,5 · 100 = 50%
Portanto:
![]()

Exercícios resolvidos
Questão 1 – (Unisinos-RS) Sabendo que a distância entre duas cidades num mapa, na escala 1 : 1 600 000, é de 8 cm, qual é a distância real entre elas?
a) 2 km
b) 12,8 km
c) 20 km
d) 128 km
e) 200 km
Solução
Alternativa d. Do enunciado temos a escala 1 : 1 600 000, ou seja, cada 1 centímetro no mapa corresponde a 1 600 000 centímetros na realidade. Interpretando tal escala como sendo a razão entre 1 e 1 600 000, devemos determinar a media real de uma distância de 8 centímetros no mapa, logo:
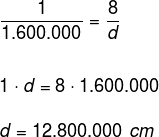
Observe que as alternativas são dadas utilizando-se a unidade de medida quilômetro. Para transformar centímetro em quilômetro, devemos dividir o último resultado por 100.000:
12.800.000 ÷ 100.000 = 128 km
Questão 2 – A razão entre a idade de duas pessoas é de 12 para 11. Sabe-se que a soma das idades é 115, determine a idade de cada uma dessas pessoas.
Solução
Como desconhecemos a idade das duas pessoas, vamos nomeá-las a e b. Como a razão entre essas idades é de 12 para 11, podemos montar uma proporção:
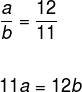
Sabemos que a soma das idades é 115, logo:
a + b = 115
a = 115 – b
Substituindo o valor de a na primeira equação, teremos:
11 · a = 12 · b
11 · (115 – b) = 12 · b
1.265 – 11b = 12b
1.265 = 12b + 11b
1.265 = 23b
b = 1.265 ÷ 23
b = 55
Como a = 115 – b, então:
a = 115 – 55
a = 60
Portanto, essas pessoas possuem, respectivamente, 60 anos e 55 anos.
Por Robson Luiz
Professor de Matemática



