Regra de três composta

A regra de três composta é um método utilizado para encontrar valores desconhecidos, quando o problema envolve grandezas que possuem proporção. É importante lembrar que existem duas possibilidades para as grandezas quando elas são proporcionais. Elas podem ser direta ou inversamente proporcionais.

Quando existem três ou mais grandezas que são proporcionais, aplicamos a regra de três composta seguindo um passo a passo para a resolução. Os passos são:

• identificação das grandezas;

• construção da tabela;

• análise da relação entre as grandezas; e

• resolução da equação gerada pelo problema.

A regra de três composta é uma extensão da regra de três simples, então, para dominar a composta, é essencial dominar a resolução da simples, que é aplicada quando há apenas duas grandezas.

Leia também: Cálculo de porcentagem com regra de três

Tópicos deste artigo

• 1 - Passo a passo para resolver uma regra de três composta
• 2 - Diferença entre regra de três simples e composta
• 3 - Exercícios resolvidos

Passo a passo para resolver uma regra de três composta

Para resolver problemas envolvendo regra de três composta, precisamos seguir alguns passos. Esses passos são os mesmos, independentemente da quantidade de grandezas envolvidas na problema.

• 1º passo: identificação das grandezas e construção da tabela.

• 2º passo: analisar a proporção que existe entre a grandeza que contém a incógnita.

• 3º passo: inverter a razão caso exista alguma grandeza inversamente proporcional à grandeza que contém a incógnita; caso não exista, ir direto para o passo quatro.

• 4º passo: montar a equação, deixando a grandeza que possui incógnita no primeiro membro da igualdade e calcular o produto entre as demais, que ficarão no segundo membro.

→ Regra de três composta com três grandezas

Exemplo:

Uma construtora foi contratada para realizar a reforma de todas as escolas do município de Cocalzinho, em Goiás. As escolas são construídas com formado e tamanho padrão nessa cidade, logo o muro externo possui a mesma medida. Sabendo que 4 pintores levariam 8 dias para pintar 6 escolas, quanto tempo 8 pintores levariam para pintar 18 escolas?

Resolução:

As grandezas são: quantidade de pintores, dias e quantidade de escolas pintadas.

Agora vamos construir a tabela, começando sempre pela grandeza que possui a incógnita:

Agora é necessário analisar a relação que existe entre as grandezas, Na regra de três composta, a comparação é feita a partir da grandeza que possui a incógnita em relação às outras, ou seja, vamos comparar dias e pintores e dias e escolas.

Para comparar dias e pintores, vamos fixar a quantidade de escolas. Em uma mesma quantidade de escolas, se eu aumento a quantidade de pintores, a quantidade de dias que eu levo para fazer a reforma diminui, logo essas grandezas são inversamente proporcionais.

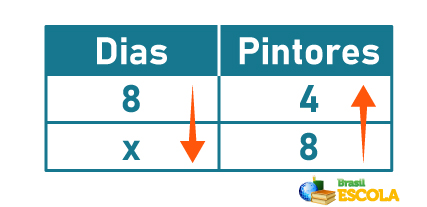
Comparando dias e escolas e fixando a quantidade de pintores, ao analisar a proporcionalidade, se o número de escolas aumenta, a quantidade de dias também aumenta.

Em resumo, temos que dias é inversamente proporcional à quantidade de pintores e diretamente proporcional à quantidade de escolas.

Para construir a equação, é necessário isolar a fração da incógnita e inverter a fração da grandeza inversamente proporcional.

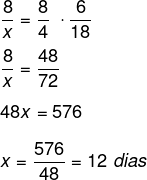
Veja também: Três erros mais cometidos no uso da regra de três

→ Regra de três composta com quatro grandezas

Para resolver problemas de regra de três composta com quatro grandezas, seguimos os mesmos passos apresentados anteriormente.

Exemplo:

Em uma fábrica de peças para caminhão, para produzir uma determinada peça, sabemos que 3 máquinas, trabalhando durante 5 dias, ligadas durante 4 horas, conseguem produzir 4.000 peças, que é a demanda mensal da fábrica. Durante o processo, uma das máquinas estragou, o que fez com que a fábrica decidisse por aumentar a quantidade de dias de produção para 6 dias, e o tempo de trabalho das máquinas para 8 horas. Qual será a quantidade de peças produzidas nessa situação?

Resolução:

As grandezas são: quantidade de máquinas, dias, horas e quantidade de peças.

Analisando as proporções entre as grandezas, comparando máquinas com peças, dias com peças e horas com peças, podemos afirmar:

• se eu aumento a quantidade de máquinas, consequentemente a produção de peças vai aumentar;

• se eu aumento a quantidade de dias de trabalho das máquinas ou mesmo de horas de trabalho, há também um aumento na quantidade de peças produzidas, sendo assim, todas as grandezas são diretamente proporcionais à quantidade de peças produzidas.

Montando a tabela, temos que:

Agora resolvendo a equação:

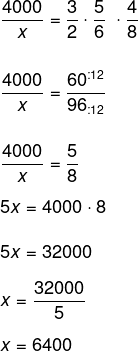
Diferença entre regra de três simples e composta

O trabalho com grandezas é bastante comum em nosso cotidiano e, quando as grandezas são direta ou inversamente proporcionais, é possível prever o que acontecerá com uma grandeza por meio da comparação entre elas.

A regra de três simples é utilizada para problemas com somente duas grandezas. Ela é aplicada quando conhecemos três valores, dois de uma grandeza e um de outra. Já a regra de três composta é aplicada em situações um pouco mais complexas, envolvendo mais de duas grandezas.

Vale ressaltar que os métodos são bastante parecidos, pois a regra de três composta nada mais é do que uma extensão da regra de três simples.

Acesse também: Três conceitos básicos de Matemática para o Enem

Exercícios resolvidos

Questão 1 – (Enem 2013) Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente.

A quantidade de ralos do novo reservatório deverá ser igual a:

A) 2
B) 4
C) 5
D) 8
E) 9

Resolução

Alternativa C.

As gradezas são: capacidade, quantidade de ralos e tempo em horas. A grandeza que contém o valor desconhecido é a quantidade de ralos, logo vamos compará-la com a capacidade e com o tempo.

Fixando o tempo, se eu aumento a quantidade de ralos, a capacidade de escoar água também vai aumentar, logo essas grandezas são diretamente proporcionais. Se eu aumento a quantidade de ralos, fixando o volume, o tempo que gastamos para escoar toda a água vai diminuir, logo ralos e tempo são inversamente proporcionais.

Montando a tabela, temos que:

Invertendo a fração e a razão das horas, temos que:

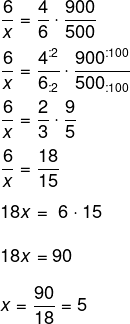
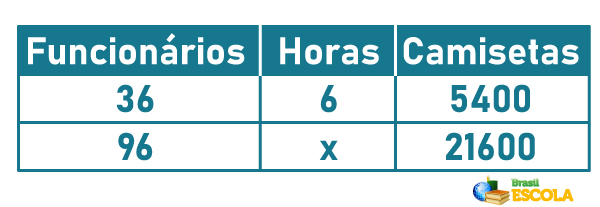
Questão 2 – (Enem 2015 – segunda aplicação) Uma confecção possuía 36 funcionários, alcançando uma produtividade de 5 400 camisetas por dia, com uma jornada de trabalho diária dos funcionários de 6 horas. Entretanto, com o lançamento da nova coleção e de uma nova campanha de marketing, o número de encomendas cresceu de forma acentuada, aumentando a demanda diária para 21 600 camisetas. Buscando atender essa nova demanda, a empresa aumentou o quadro de funcionários para 96. Ainda assim, a carga horária de trabalho necessita ser ajustada.

Qual deve ser a nova jornada de trabalho diária dos funcionários para que a empresa consiga atender a demanda?

A) 1 hora e 30 minutos.
B) 2 horas e 15 minutos.
C) 9 horas.
D)16 horas.
E) 24 horas

Resolução

Alternativa C.

As grandezas são: número de funcionários, número de camisetas e tempo em horas por dia. A incógnita está na grandeza horas por dia, então vamos analisar a proporção dela com as demais grandezas:

• fixando o número de camisetas, se eu aumento a quantidade de funcionários, o tempo de trabalho por dia diminui, logo funcionários e horas é inversamente proporcional;

• fixando o número de funcionários, se eu diminuir as horas trabalhadas por dia, consequentemente o número de camisetas diminuirá, logo essas grandezas são diretamente proporcionais.

Montando as razões e invertendo a razão dos funcionários, temos que:

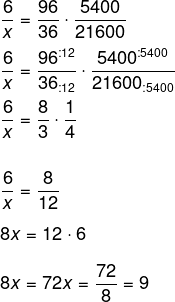
Por Raul Rodrigues de Oliveira
Professor de Matemática