Algumas situações envolvendo porcentagem podem ser resolvidas por meio de uma regra de três simples. Entendemos por porcentagem uma razão centesimal (fração com denominador igual a 100) que é denominada de taxa percentual e é representada pelo símbolo % (por cento). Por exemplo, se temos 45%, podemos representá-lo das seguintes formas:
45% = 45
100
ou
9
20
ou 0,45
Sempre que utilizarmos a regra de três no intuito de determinar porcentagens, devemos relacionar a parte do todo com o valor de 100%.
Obs.: Nas situações envolvendo uma porcentagem, realizamos a multiplicação cruzada por ser uma grandeza diretamente proporcional.
Exemplos
1º) Determine o valor de 95% de R$ 105,00
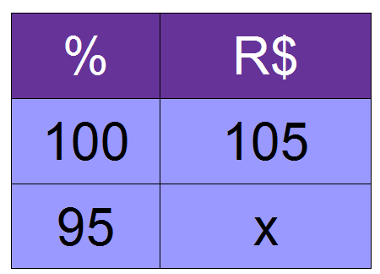
100x = 95·105
100x = 9975
x = 9975
100
x = 99,75 reais
Portanto, 95% de R$ 105,00 é igual a R$ 99,75.
2º) Em uma sala de 40 alunos, foi realizada uma pesquisa, a qual apontou que 30 alunos gostam de praticar esportes. Qual é a porcentagem de alunos que gostam de esportes?
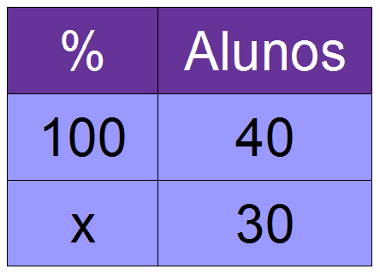
40x = 100 * 30
40x = 3000
x = 3000
40
x = 75%
Temos que 75% dos alunos dessa classe gostam de esportes.
3º) Pedro acertou 21 questões de uma prova, que correspondem a 70% do total de questões. Quantas questões tinha a prova?
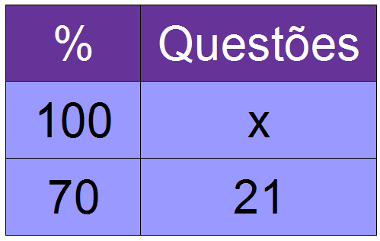
70x = 21*100
70x = 2100
x = 2100
70
x = 30
A prova tinha 30 questões.
4º) Em uma promoção, o preço de um objeto foi reduzido de R$ 76,00 para R$ 57,00. Calcule o valor do desconto em porcentagem.
Devemos primeiramente determinar o valor real do desconto: 76 – 57 = 19. Ao compararmos o valor do desconto com o valor sem o desconto, obtemos o valor percentual.
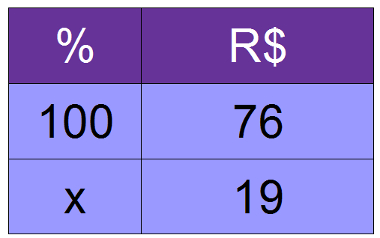
76x = 100 * 19
76x = 1900
x = 1900
76
x = 25%
O desconto dado foi de 25%.
5º) Uma conta de restaurante, incluindo os 10% de serviço, ficou em R$ 143,00. Qual o valor da conta sem a taxa de serviço?
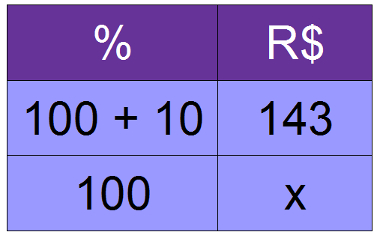
110x = 143 * 100
110x = 14300
x = 14300
110
x = 130
A conta sem o valor do serviço é de R$ 130,00.
6º) Um produto que custava R$ 80,00 foi reajustado em 25%. Determine o novo valor do produto.
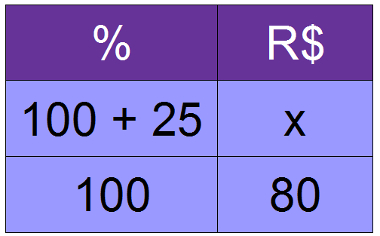
100x = 125 * 80
100x = 10000
x = 100
O preço do produto após o reajuste é de R$ 100,00.
7º) O preço de um computador é de R$ 2.200,00. Qual será o preço do computador caso ele sofra um reajuste de 18%?
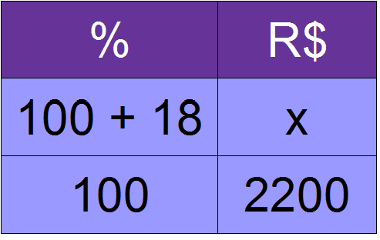
100x = 2200 * 118
100x = 259600
x = 259600
100
x = 2 596
Caso aconteça o reajuste de 18%, o computador passará a custar R$ 2 596,00.
8º) Considerando que a população de um país é de cerca de 180 milhões de habitantes e que 38 milhões são considerados fumantes, qual a porcentagem de fumantes no país referido?

180x = 3800
x = 3800
180
x = 21,1
A porcentagem de fumantes no país referido é de aproximadamente 21,1%.
Por Marcos Noé
Graduado em Matemática






