As grandezas inversamente proporcionais estão presentes em muitas situações do nosso cotidiano. Em matemática ou física, chamamos de grandeza tudo aquilo que podemos medir, mensurar ou quantificar. Na maioria dos casos que vamos estudar aqui, veremos que essas grandezas relacionam-se, isto é, à medida que uma delas varia, a outra varia também, isso pode ocorrer de forma direta ou inversamente proporcional. São exemplos de grandezas que se relacionam: velocidade, espaço, tempo, massa, força, aceleração etc.
Leia também: Propriedade da proporção
Tópicos deste artigo
- 1 - Como saber se o número é inversamente proporcional?
- 2 - Exemplos de grandezas inversamente proporcionais
- 3 - Outros exemplos
- 4 - Exercício
Como saber se o número é inversamente proporcional?
As grandezas são ditas como inversamente proporcionais quando uma delas aumenta e a outra necessariamente diminui, ou o oposto. O mesmo ocorre com os números separadamente. Considere os números a, b, c e d com b ≠ 0 e d ≠ 0. Dizemos que esses números a e b são inversamente proporcionais aos números c e d, nessa ordem, se:
![]()
-
Exemplos
a) Verifique se os números 36, 24, 2 e 3 são inversamente proporcionais nessa ordem.
Para isso, é preciso que a razão entre o primeiro e o inverso do terceiro seja igual à razão entre o segundo e o inverso do quarto. Em seguida, realizando a multiplicação cruzada, temos:
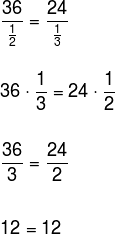
Como a igualdade é verdadeira, os números são inversamente proporcionais.
b) Verifique se os números 2, 3, 5 e 6 são inversamente proporcionais.
De modo análogo, temos:
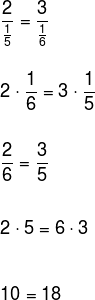
Como a igualdade não é verdadeira, temos que os números não são inversamente proporcionais.
Veja também: Três erros cometidos na regra de três
Exemplos de grandezas inversamente proporcionais
No início do texto, foi dito que quando duas grandezas relacionam-se ou elas são diretamente proporcionais ou inversamente proporcionais, pois bem, quando duas ou mais grandezas são diretamente proporcionais, no momento que uma delas aumenta, todas as outras também aumentarão. Por exemplo, quanto maior é a quantidade de farinha (↑) em uma padaria, maior é a quantidade produzida de pão (↑). Desse modo, quantidade de farinha e número de pães são grandezas diretamente proporcionais.
Agora, duas ou mais grandezas serão inversamente proporcionais caso uma delas aumente e a outra diminua, e vice-versa. Por exemplo, imagine um trem indo de uma estação para outra, quanto maior for a velocidade do trem (↑), menor será o tempo de viagem (↓), logo, as grandezas velocidade e tempo são inversamente proporcionais.
Outros exemplos
→ Quanto mais torneiras (↑) utilizamos para encher um tanque, menor o tempo de enchimento (↓).
→ Quanto mais ônibus (↑) uma empresa coloca para levar uma quantidade específica de pessoas, menor será a quantidade de viagens feitas (↓).

Exercício
Questão 1 – Divida o número 51 em três partes inversamente proporcionais aos números 9, 5 e 3.
Solução
Como não sabemos quais são as partes pelas quais vamos dividir o número 51, vamos chamá-las de a, b e c. Assim temos que:
a + b + c = 51
Dividindo o 51 em três partes inversamente proporcionais aos números 9, 5 e 3, temos que:
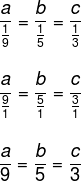
Observe que, por enquanto, somente realizamos a divisão de frações em cada uma das partes. Como todas as frações são iguais, elas representam a mesma quantidade, logo, vamos chamar cada uma delas de x, em que x representa essa mesma quantidade.
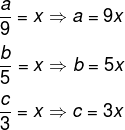
Substituindo os valores de a, b e c na expressão, temos:
a + b + c = 51
9x + 5x + 3x = 51
17x = 51
x = 3
E por último, substituindo o valor de x em a, b e c, segue que:
a = 9x → a = 9 (3) → a = 27
b = 5x → b = 5 (3) → b = 15
c = 3x → c = 3 (3) → c = 9
Por Robson Luiz
Professor de Matemática



