Juros compostos

Os juros compostos são recorrentes nas relações comerciais, nas compras parceladas a longo prazo, nos investimentos, nos empréstimos e até mesmo no simples atraso do pagamento de contas. O juros pode ser um aliado ou um vilão. É importante dominar os fatores que influenciam o seu cálculo, que são o capital, a taxa de juros, o tempo e o montante.

Ao comparar o juros composto com o juros simples, precisamos entender que o primeiro é calculado sempre sobre o valor do exercício anterior, já o segundo é calculado sempre em cima do valor inicial. O juros composto terá maior crescimento com o passar do tempo, em comparação com o juros simples.

Veja também: Proporção – igualdade entre duas razões

Tópicos deste artigo

• 1 - Fórmula do juros composto
• 2 - Como calcular os juros compostos?
  • Encontrando montante e juros
  • Encontrando o tempo
  • Encontrando a taxa de juros
• 3 - Diferença entre juros simples e juros compostos
• 4 - Exercícios resolvidos

Fórmula do juros composto

O cálculo do juros composto é dado por esta fórmula:

Cada uma dessas letras é um importante conceito da matemática financeira:

• Capital (C): é o primeiro valor investido. Conhecemos como capital o valor inicial da negociação, ou seja, ele é o valor de referência para calcularmos os juros com o passar do tempo.

• Juros (J): é o valor de compensação para o rendimento. Quando uma instituição financeira faz um empréstimo, ela está abdicando-se de estar com esse dinheiro em um determinado prazo, porém, quando ela for recebê-lo, seu valor será corrigido pelo que chamamos de juros, e é com base nele que a empresa vê uma compensação pelo empréstimo. Em um investimento, trata-se do valor dos rendimentos adquiridos.

• Taxa de juros (i): é a porcentagem cobrada em cima do capital a cada instante. Essa taxa pode ser ao dia (a.d.), ao mês (a.m.), ao bimestre (a.b.) ou ao ano (a.a.). A taxa de juros é uma porcentagem geralmente representada na forma percentual, porém, para calcular-se o juros composto, é importante escrevê-la sempre na forma decimal.

• Tempo (t): é o tempo em que o capital ficará aplicado. É importante que a taxa de juros (i) e o tempo (t) estejam sempre na mesma unidade de medida.

• Montante (M): é o valor final da transação. O montante é calculado pela soma do capital com os juros — M = C + J.

Como calcular os juros compostos?

Saber manipular a fórmula é fundamental para o estudo dos juros compostos. Como há quatro variáveis (montante, capital, taxa de juros e tempo), os problemas que envolvem esse tema podem dar o valor de três delas e sempre pedir o cálculo da quarta variável, podendo ser qualquer uma delas. Por isso o domínio de equações é fundamental para a resolução de problemas que envolvem juros compostos.

Vale ressaltar que, para calcular-se os juros, é necessário conhecer o capital e o montante, pois o juros é dado pela diferença dos dois, ou seja:

• Encontrando montante e juros

Exemplo

Um capital de R$1400 foi aplicado a juros compostos em um fundo de investimento que rende 7% a.a. Qual será o juros acumulado após 24 meses?

Resolução

Dados importantes: C = 1400; i = 7% a.a.; t = 24 meses.

Note que o tempo e a taxa estão em unidades diferentes, mas sabemos que 24 meses é igual a 2 anos, logo, t = 2 anos, e que a taxa precisa ser escrita na forma decimal, i = 0,07.

M = C (1 + i) ^t

M = 1400 (1 + 0,07)²

M = 1400 (1,07)²

M = 1400 . 1,1449

M = 1602,86.

Para encontrar o juros temos que:

J = M – C

1602,86 – 1400 = 202,86

• Encontrando o tempo

Exemplo

Quanto tempo um capital de R$1500 aplicado a juros compostos, com taxa de 10% a.a, leva para gerar um montante de R$1996,50?

Resolução

Como t é uma potência, encontraremos uma equação exponencial que pode ser resolvida por fatoração ou, em muitos casos, só por logaritmo. Como nem sempre trata-se de números inteiros, o recomendado para esses problemas é que se use calculadora científica. No caso de vestibulares e provas de concurso, o valor do logaritmo é dado na questão.

Dados:

C = 1500 M = 1996,50 i = 10% = 0,01

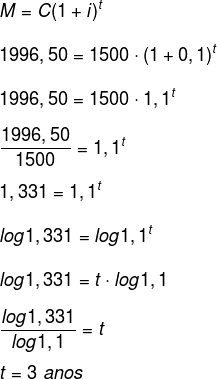
• Encontrando a taxa de juros

Exemplo

Qual é a taxa de juros aplicada ao ano para que um capital de R$800 gere um juros de R$352 em dois anos?

Resolução

Dados: C = 800; t = 2 anos; J = 352.

Para encontrar a taxa, precisamos primeiro encontrar o montante.

M = C + J

800 + 352 = 1152

Agora temos que:

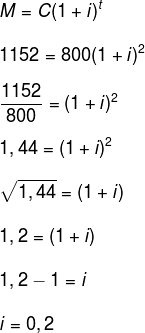
Em forma percentual, podemos dizer também que i = 20%

Leia também: Grandezas inversamente proporcionais – relação como a de velocidade e tempo

Diferença entre juros simples e juros compostos

Os juros simples utilizam uma fórmula diferente da apresentada para os juros compostos:

A diferença entre o comportamento dos juros simples e o dos juros compostos, a curto prazo, é bastante sutil, mas, no decorrer do tempo, os juros compostos são bem mais vantajosos.

Acontece que o juros simples é sempre calculado sobre o valor inicial da transação. Por exemplo, se você aplica R$500 com juros simples de 10 % ao mês, isso significa que todo mês aquele capital renderá 10 % de R$500, ou seja, R$50, independentemente do tempo que ele permanecer lá. O juros simples é comum para o atraso de contas, como de água e energia. A cada dia de atraso, a soma dá-se com um valor fixo calculado em cima da conta.

Já o juros composto, pensando no mesmo valor e na mesma taxa, no primeiro mês, seu rendimento é calculado em cima do valor anterior. Por exemplo, no primeiro mês, os 10% serão calculados em cima dos R$500, gerando R$50 de juros e um montante de R$550. No próximo mês, os 10 % serão calculados em cima do valor atual do montante, ou seja, 10 % de R$550, gerando um juros de R$55, e assim sucessivamente. Dessa forma, para investimentos, o juros composto é mais vantajoso. Ele é bastante comum exatamente nesse segmento de investimentos, como a poupança.

Veja a tabela comparativa do mesmo valor rendendo a 10 % a.m durante um ano a juros simples e a juros composto.

Exercícios resolvidos

Questão 1 - Quanto conseguirei se investir um capital de R$2000 a juros composto, de 3% a.a., durante um período de 48 meses?

Resolução
Dados: C = 2000,00

i = 3% a.a.

t = 48 meses = 4 anos (note que a taxa está em anos)

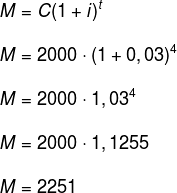
Questão 2 - Para investir R$25.000, Maria cotou duas opções:

• 5% a.m. a juros simples

• 4% a.m a juros composto

A partir de quanto tempo a segunda opção é mais vantajosa?

Resolução
Para realizar a comparação, segue a tabela do cálculo dos juros da primeira e da segunda opção:

Ao comparar as duas opções, percebe-se a segunda como mais vantajosa para investimentos acima de 11 meses.

Por Raul Rodrigues de Oliveira
Professor de Matemática