Medidas de comprimento

As unidades de medidas de comprimento surgem para suprir a necessidade do ser humano de medir vários tipos de distâncias. Existem várias unidades de medidas de comprimento, a utilizada no sistema internacional de unidades é o metro, e seus múltiplos (quilômetro, hectômetro e decâmetro) e submúltiplos (decímetro, centímetro milímetro).

Além das unidades de medidas de comprimento apresentadas, existem outras como as que utilizam o corpo como parâmetro: o palmo, o pé, a polegada. Ainda, há aquelas que não são do sistema internacional, mas são utilizadas a depender da região, como a légua, a jarda, a milha e o ano-luz.

Leia também: Medidas de massa – unidades de medida e conversão

Tópicos deste artigo

• 1 - Quais são as unidades de medidas de comprimento?
• 2 - Conversão das medidas de comprimento
• 3 - Outras unidades de medidas de comprimentos
• 4 - Exercícios resolvidos

Quais são as unidades de medidas de comprimento?

Medir a distância entre dois pontos de referência é uma tarefa executada pelos seres humanos desde as primeiras civilizações. Inicialmente utilizávamos objetos do dia a dia como referenciais, como cordas ou o próprio corpo humano. Adotado como medida fundamental para distância no sistema internacional de unidades, a comunidade científica utiliza o metro como referência para medir-se comprimentos.

Para medir-se distâncias maiores, existem o que chamamos de múltiplos do metro, que são:

• decâmetro: 1 decâmetro corresponde a 10 metros,

• hectômetro: 1 hectômetro corresponde a 100 metros,

• quilômetro: 1 quilômetro corresponde a 1000 metros.

Para medir-se a distância, por exemplo, entre duas cidades, é mais conveniente usar-se quilômetros em vez de metros.

Para medir-se distâncias menores, existem os submúltiplos do metro, que são:

• decímetro: 10 decímetros correspondem a 1 metro.

• centímetro: 100 centímetros corresponde a 1 metro

• milímetro: 1000 milímetros corresponde a 1 metro.

Para objetos menores, como talheres, é mais conveniente utilizarmos como unidade de medida o centímetro em vez do metro.

Os múltiplos e submúltiplos do metro são representados por siglas:

quilômetro → km

hectômetro → hm

decâmetro → dam

metro → m

decímetro → dm

centímetro → cm

milímetro → mm

Conversão das medidas de comprimento

Para realizar a conversão, precisamos construir a seguinte tabela, respeitando a ordem para os múltiplos e submúltiplos do metro:

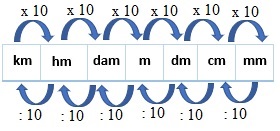
Para realizar a conversão de uma unidade que está à esquerda para outra que está à direita, multiplicamos por 10 cada unidade de medida.

• Exemplo:

Convertendo 1,2 m → cm

Ao analisar-se a tabela, de metro até centímetro, há duas unidades de medida

m→ dm → cm. Então multiplicaremos por 10 cada uma.

1,2 · 10 · 10 = 1,2 · 100 = 120 cm

Para realizar conversões da direita para a esquerda, dividimos por 10 para cada unidade de medida.

• Exemplo 2:

Convertendo 7 500 mm → dam

Ao analisar-se a tabela, de milímetro para decâmetro, há quatro unidades de medida.

dam ← m ← dm ← cm ← mm

7500 : 10 : 10 : 10 : 10 = 7500 : 10 000 = 0,75 dam

Veja também: Critérios de divisibilidade – propriedades que facilitam a operação de divisão

Outras unidades de medidas de comprimentos

Existem outras unidades de medidas de comprimento bastante comuns, sendo elas:

• Polegada: utilizada para medir-se tela de smartphone, notebook e demais aparelhos eletrônicos. É denotada geralmente pelo número seguido de duas aspas, por exemplo 40” (lê-se: 40 polegadas). Uma polegada corresponde a 2,54 cm.

• Palmo: utilizado para medir-se objetos um pouco maiores do que os que medimos com polegadas, e é pouco usado atualmente. Um palmo corresponde a 22,86 cm.

• Pé: utilizado até hoje para situar-se quanto à altura de um avião. Para representar uma distância medida em pés, colocamos o número seguido de uma aspa, por exemplo 30’(lê-se: 30 pés). Um pé corresponde a 30,48 cm.

• Jarda: utilizada nos EUA, sendo comum no futebol americano. Uma jarda corresponde a 0,9144 m.

• Légua: utilizada antigamente para medir-se distâncias maiores, a légua era bastante comum na navegação. Uma légua corresponde a 4,82803 quilômetros.

• Milha: utilizada para medir-se distâncias maiores, tendo sido bastante comum nos povos antigos. Uma milha corresponde a 1,60934 km.

• Ano-luz: utilizado para medir-se a distância entre astros, sendo muitas vezes confundido com medida de tempo. Um ano-luz corresponde a 9 460 730 472 580,8 km.

Exercícios resolvidos

Questão 1 - (Enem) Um mecânico de uma equipe de corrida necessita que as seguintes medidas realizadas em um carro sejam obtidas em metros:

a) distância a entre os eixos dianteiro e traseiro;

b) altura b entre o solo e o encosto do piloto.

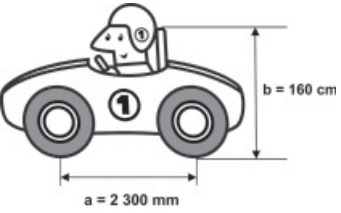
Ao optar-se pelas medidas a e b em metros, obtêm-se, respectivamente,

a) 0,23 e 0,16.
b) 2,3 e 1,6.
c) 23 e 16.
d) 230 e 160.
e) 2300 e 1600.

Resolução

Alternativa B

Convertendo-se a medida de a = 2 300 mm → m

m ← dm ← cm ← mm

Para cada unidade de medida à esquerda, dividimos por 10, logo, dividiremos o valor de a por 1000.

2300 : 1000 = 2,3 metros

Dessa forma, a medida a = 2,3 metros

Convertendo-se a medida de b = 160 cm → m
m ← dm ← cm

Como vamos andar duas unidades de medidas à esquerda, dividiremos por 100.

160 : 100 = 1,6

b = 1,6 m

Durante uma partida de futebol americano, um jogador percorreu 22 jardas consecutivas. Sabendo que 1 jarda corresponde a 0,91 metros, essa distância em jardas é igual a, aproximadamente:

a) 25,09 metros

b) 30 metros

c) 20,02 metros

d) 23,12 metros

e) 24,18 metros

Resolução

Alternativa C.

Sabendo que ele percorreu 22 jardas, basta realizarmos a multiplicação:

22 x 0,91 = 20,02

 

Por Raul Rodrigues de Oliveira
Professor de Matemática