O tronco de um cone é o sólido formado pela parte inferior do cone ao realizarmos uma secção em qualquer altura paralela à base. Quando cortamos o cone em uma altura qualquer, ele é dividido em dois sólidos geométricos, um cone menor do que o anterior e o tronco de um cone.
O tronco do cone possui fórmulas específicas para que seja possível calcular a área total e o volume desse sólido geométrico.
Leia também: Quais são os sólidos de Platão?
Tópicos deste artigo
- 1 - Elementos do tronco de cone
- 2 - Geratriz do tronco de cone
- 3 - Volume do tronco de cone
- 4 - Planificação do tronco de um cone
- 5 - Área total do tronco de cone
- 6 - Exercícios resolvidos
Elementos do tronco de cone

O tronco de um cone é um caso especial de corpos redondos. Ele recebe esse nome porque, em um cone, quando realizamos uma secção paralela à base, ele é dividido em duas partes. A parte que está embaixo é o tronco do cone.
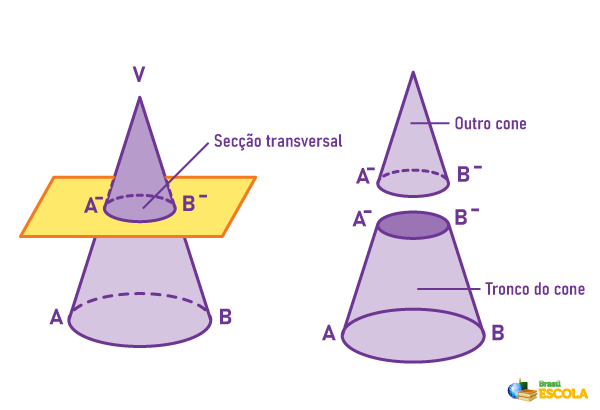
Dado o tronco de um cone, existem elementos importantes nesse sólido, que recebem nomes específicos.
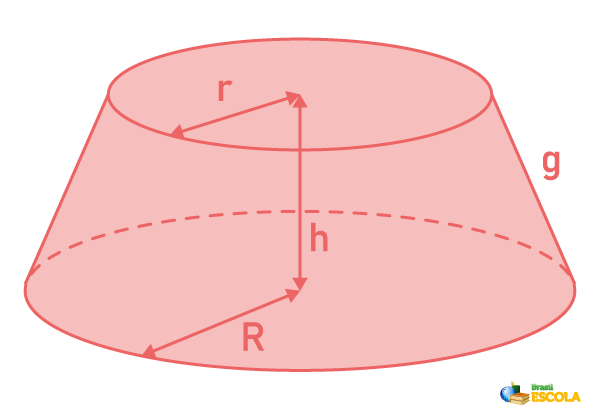
R → raio da base maior
h → altura do cone
r → raio da base menor
g → geratriz do tronco de cone
Podemos perceber que o tronco do cone é composto por duas faces no formato de círculo, as quais são conhecidas como bases. Além disso, uma delas possui sempre raio menor que o da outra. Assim, r < R e, consequentemente, há uma base maior e uma base menor.
Geratriz do tronco de cone
Dado um tronco de cone, é possível calcular o valor da geratriz desse sólido utilizando o teorema de Pitágoras, quando conhecemos os raios da base maior e menor, além da altura.
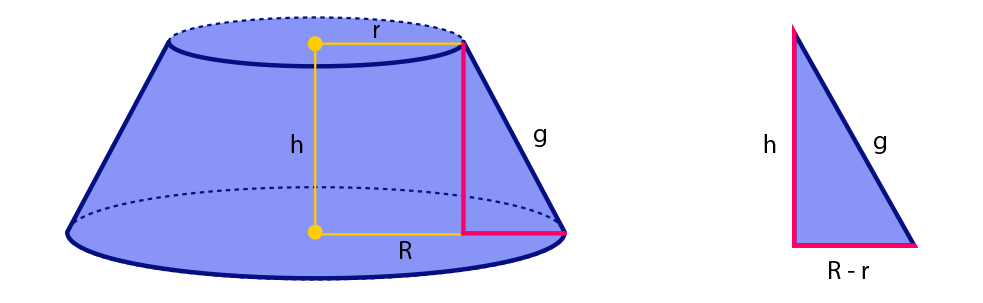
g² = h² + (R – r)²
Exemplo:
Encontre a geratriz de um tronco de cone que possui altura igual a 8 cm, raio da base maior igual a 10 cm e raio da base menor igual a 4 cm.
Para encontrar a geratriz do tronco do cone, temos que:
h = 8
R = 10
r = 4
Substituindo na fórmula:
g² = h² + (R – r)²
g² = 8² + (10 – 4)²
g² = 64 + 6²
g² = 64 + 36
g² = 100
g = √100
g = 10 cm
Veja também: Como encontrar o centro de uma circunferência?
Volume do tronco de cone
Para calcular o volume do tronco do cone, utilizamos a fórmula:
![]()
Conhecendo os valores da altura, do raio da base maior e do raio da base menor, é possível calcular o volume do tronco de um cone.
Exemplo:
Encontre o volume de um tronco de cone que possui altura igual a 6 cm, raio da base maior igual a 8 cm e raio da base menor igual a 4 cm. Use π = 3,1.
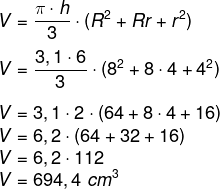
Planificação do tronco de um cone
A planificação de um sólido geométrico é a representação das suas faces de forma bidimensional. Veja a seguir a planificação do tronco de cone.
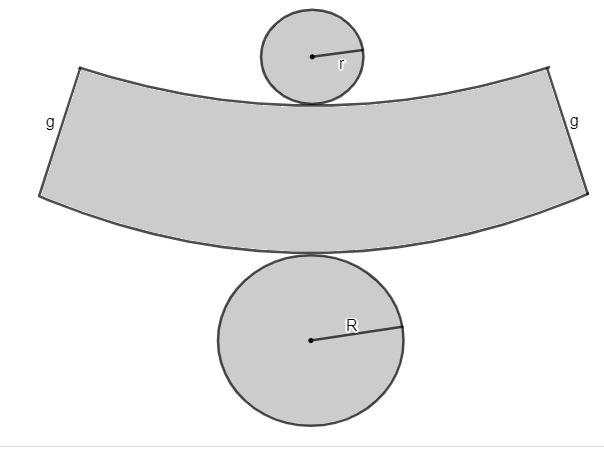
Área total do tronco de cone
Conhecendo a planificação de um tronco de cone, é possível calcular o valor da área total desse sólido geométrico. Sabemos que ele é composto por duas bases no formato de um círculo e também pela sua área lateral. A área total do tronco de um cone é a soma das áreas dessas três regiões:
AT = AB + Ab + Al
AT → área total
AB → área da base maior
Ab → área da base menor
AL → área lateral
Note que as bases são círculos e que a área lateral parte de uma circunferência, então:
Al = πg (R + r)
AB = πR²
Ab = πr²
Exemplo:
Calcule a área total do tronco de cone que possui altura igual a 12 cm, raio da base maior igual a 10 cm e raio da base menor igual a 5 cm. Use π = 3.
Primeiro encontraremos a geratriz para calcular a área lateral:
g² = 12² + (10 – 5)²
g² = 12² + 5²
g² = 144 + 25
g² = 169
g = √169
g = 13
Al = πg (R + r)
Al = 3 · 13 (10 + 5)
Al = 39 · 15
Al = 39 · 15
Al = 585 cm²
Agora calcularemos a área de cada uma das bases:
AB = πR²
AB = 3 · 10²
AB = 3 · 100
AB = 300 cm²
Ab = πr²
Ab = 3 · 5²
Ab = 3 · 25
Ab = 75 cm²
AT = AB + Ab + Al
AT = 300 + 75 + 585 = 960 cm²
Veja também: Quais as diferenças entre círculo e circunferência?
Exercícios resolvidos
Questão 1 – (Enem 2013) Uma cozinheira, especialista em fazer bolos, utiliza uma forma no formato representado na figura:
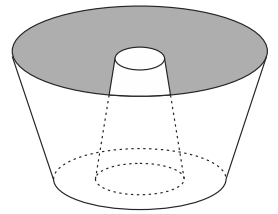
Nela se identifica a representação de duas figuras geométricas tridimensionais. Essas figuras são:
A) um tronco de cone e um cilindro.
B) um cone e um cilindro.
C) um tronco de pirâmide e um cilindro.
D) dois troncos de cone.
E) dois cilindros.
Resolução
Alternativa D. Analisando os sólidos geométricos, os dois possuem duas faces circulares de tamanhos diferentes, logo são troncos de cone.
Questão 2 – (Nucepe) Como é e para que serve prioritariamente uma xícara todos sabemos: servir bebidas, especialmente quentes. Mas de onde surgiu a ideia de criar um "copo com alça"?
O chá, que tem origem oriental, era inicialmente servido em potes redondos, sem alças. Segundo a tradição, isso era até mesmo um alerta para quem conduzia a cerimônia da bebida: Caso o recipiente queimasse as pontas dos dedos, estava quente demais para ser ingerido. Na temperatura ideal, ela não incomodava, mesmo com o contato direto com a porcelana.
Fonte: http://www.mexidodeideias.com.br/viagem/a-historia-da-xicara. Acesso em 06/01/2018.
Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura abaixo. Qual o volume máximo, aproximado, de líquido que ela pode conter?
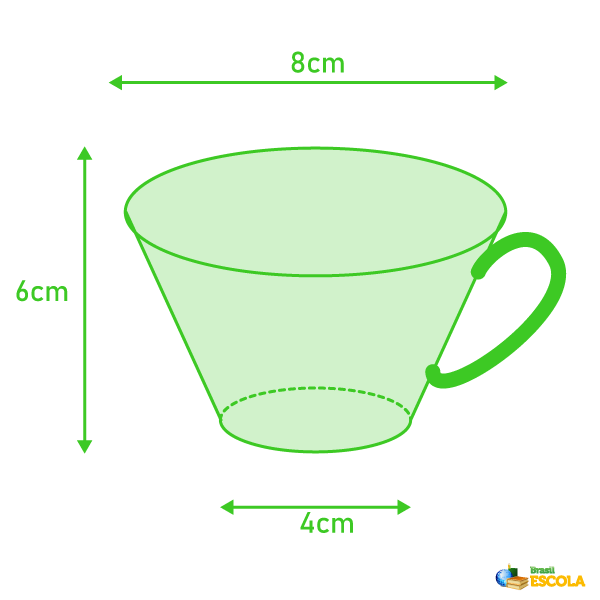
A) 168 cm³
B) 172 cm³
C) 166 cm³
D) 176 cm³
E) 164 cm³
Resolução
Alternativa D.
Para encontrar o volume, primeiro vamos calcular o valor de cada um dos raios. Para isso, basta dividir o diâmetro por dois.
R = 8/ 2 = 4
r = 4/2 = 2
Além do raio, sabemos que h = 6.
Então, temos que:
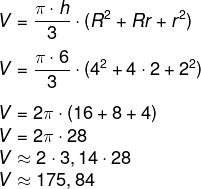
O valor mais próximo é 176 cm³.
Por Raul Rodrigues de Oliveira
Professor de Matemática





