O teorema de Pitágoras é uma relação entre as medidas dos lados de um triângulo retângulo. De acordo com esse teorema, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos. Ou seja, se os catetos medem a e b e a hipotenusa mede c, então \(c^2=a^2+b^2\).
Podemos utilizar essa relação para obter a medida de um dos lados do triângulo retângulo, supondo que os outros dois sejam conhecidos. Ainda que tal aplicação seja simples, o teorema de Pitágoras é um recurso fundamental em diversos campos da Matemática, sendo amplamente estudado durante séculos.
Leia também: Quais são os pontos notáveis de um triângulo?
Tópicos deste artigo
- 1 - Resumo sobre teorema de Pitágoras
- 2 - Videoaula sobre teorema de Pitágoras
- 3 - Fórmula do teorema de Pitágoras
- 4 - Como aplicar o teorema de Pitágoras?
- 5 - Demonstração do teorema de Pitágoras
- 6 - Triângulo pitagórico
- 7 - Teorema de Pitágoras e os números irracionais
- 8 - Quem foi Pitágoras?
- 9 - Mapa Mental: Teorema de Pitágoras
- 10 - Exercícios resolvidos sobre teorema de Pitágoras
Resumo sobre teorema de Pitágoras
-
Em um triângulo retângulo, se a e b são as medidas dos catetos e c é a medida da hipotenusa, então, pelo teorema de Pitágoras, \(c^2=a^2+b^2\).
-
O teorema de Pitágoras é útil em muitas situações, inclusive para demonstrar outros resultados matemáticos.
-
A aplicação imediata desse teorema ocorre pela substituição das medidas de dois lados conhecidos em um triângulo retângulo para obter a medida do terceiro.
-
Devido à sua importância, existem centenas de demonstrações para o teorema de Pitágoras.
Não pare agora... Tem mais depois da publicidade ;)
Videoaula sobre teorema de Pitágoras
Fórmula do teorema de Pitágoras
Em um triângulo retângulo, os catetos são os lados que formam o ângulo reto e hipotenusa é o lado oposto ao ângulo reto. Considere um triângulo retângulo em que os catetos medem a e b e a hipotenusa mede c.
O teorema de Pitágoras determina que o quadrado da medida da hipotenusa (\(c^2\)) é igual à soma dos quadrados das medidas dos catetos (\(a^2+b^2\)). Portanto, a fórmula do teorema de Pitágoras é \(c^2=a^2+b^2\).
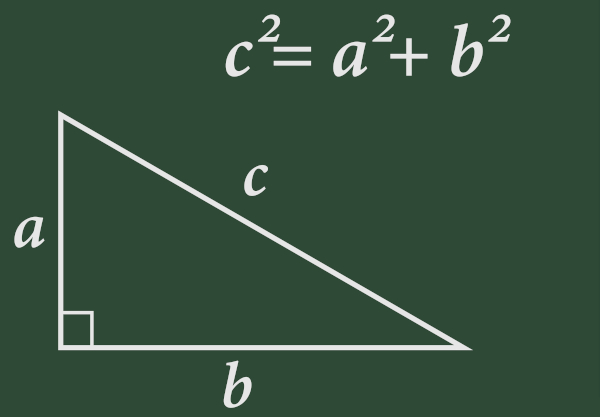
Como aplicar o teorema de Pitágoras?
Utilizamos o teorema de Pitágoras em diversos estudos geométricos, inclusive para provar outros teoremas matemáticos. Neste texto, porém, vamos nos concentrar em sua aplicação mais direta, que é determinar um dos lados de um triângulo retângulo por meio dos outros dois.
-
Exemplo:
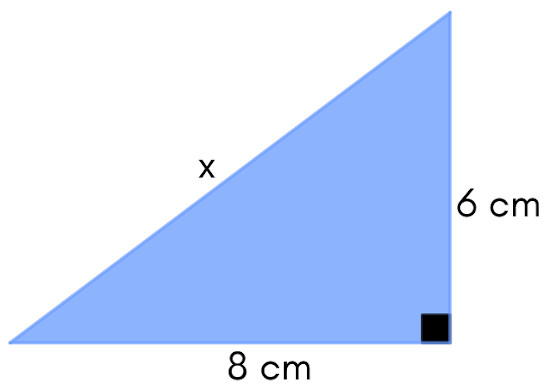
Determine o valor de x no triângulo retângulo abaixo.
Resolução:
Perceba que x é a medida da hipotenusa. Assim, pelo teorema de Pitágoras:
\(x^2=6^2+8^2\)
\(x=\sqrt{100}\)
\(x = 10\ cm\)
Demonstração do teorema de Pitágoras
A demonstração de um teorema é a verificação de sua validade, ou seja, é uma sequência de argumentos matemáticos que garantem a aplicação do teorema. No caso do teorema de Pitágoras, existem centenas de demonstrações. A seguir, realizaremos uma demonstração por semelhança de triângulos.
ABC é um triângulo retângulo com catetos de medida a e b e hipotenusa de medida c. Considere um ponto D tal que CD é a altura do triângulo relativa à hipotenusa AB.
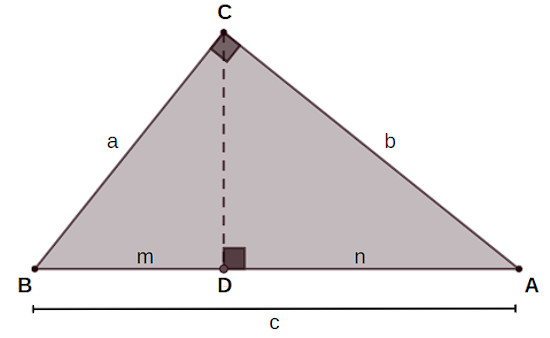
Perceba que há três triângulos retângulos nessa figura: o triângulo original ABC e os triângulos CBD e CAD, formados pelo segmento CD.
O triângulo ABC possui um ângulo reto em \(\hat{C}\), o ângulo \(\hat{A}\) e o ângulo \(\hat{B}\). Pelo caso de semelhança ângulo-ângulo (AA), os triângulos menores são semelhantes ao ABC:
-
O triângulo CBD possui um ângulo reto em \(\hat{D}\) e o ângulo \(\hat{B}\).
-
O triângulo CAD possui um ângulo reto em \(\hat{D}\) e o ângulo \(\hat{A}\).
Logo, concluímos que os três triângulos são semelhantes entre si, cada um com um ângulo reto, um ângulo de medida igual a \(\hat{A}\) e outro ângulo de medida igual a \(\hat{B}\). Atenção para a ordem de semelhança:
\(ABC \sim CBD \sim ACD\)
Consequentemente, temos a proporcionalidade entre os lados desses triângulos.
-
Nos triângulos ABC e CBD:
\(\frac{c}a=\frac{a}m\)
\(a^2=c\cdot m\)
-
Nos triângulos ABC e ACD:
\(\frac{c}b=\frac{b}n\)
\(b^2=c\cdot n\)
Somando as duas expressões, temos que:
\(a^2+b^2=c\cdot m + cn\)
\(a^2+b^2=c·(m+n)\)
Como \(m+n=c\),
\(a^2+b^2=c^2\)
Ou seja, obtemos, por meio de um triângulo retângulo, o teorema de Pitágoras.
Triângulo pitagórico
Um triângulo retângulo é chamado de pitagórico se as medidas de seus lados são números inteiros. Há evidências antigas do estudo desses triângulos, como a tábua de argila Plimpton 322 (cerca de 1800 a.C.) e a placa circular Si.427 (entre 1900 e 1600 a.C.).
Conhecer as medidas dos principais triângulos pitagóricos é uma estratégia para encontrar rapidamente um dos lados de um triângulo retângulo. O exemplo mais conhecido de triângulo pitagórico é o triângulo com catetos de medida 3 e 4 e hipotenusa de medida 5.
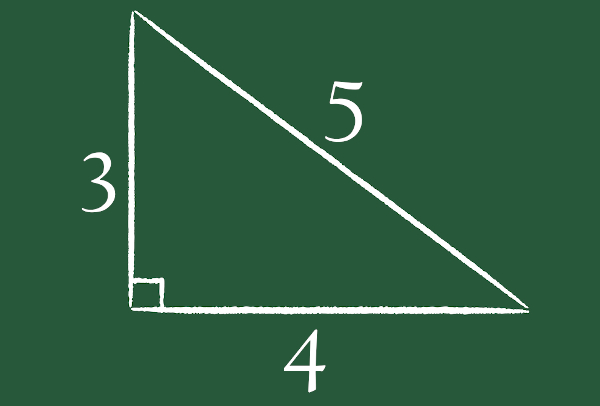
Os múltiplos dessas medidas também formam triângulos pitagóricos. Por exemplo, é possível construir um triângulo retângulo com catetos de medida 6 e 8 e hipotenusa de medida 10.
As sequências que formam os lados desses triângulos são chamadas de triplas pitagóricas (ou ternos pitagóricos), como (3, 4, 5). Outros exemplos de triplas pitagóricas são (5, 12, 13) e (7, 24, 25). Ainda que seja interessante conhecer as triplas pitagóricas, não é necessário decorá-las, uma vez que todas são obtidas com a aplicação do teorema de Pitágoras.
Saiba mais: Teorema de Tales — um teorema usado para a melhor compreensão da proporcionalidade
Teorema de Pitágoras e os números irracionais
Se considerarmos um quadrado com lado 1 e desenharmos uma das diagonais, o quadrado é dividido em dois triângulos retângulos. Perceba que cada um desses triângulos retângulos possui catetos medindo 1 e que a hipotenusa coincide com a diagonal do quadrado original.
Aplicando o teorema de Pitágoras em um dos triângulos retângulos, podemos determinar a medida da hipotenusa (ou seja, da diagonal do quadrado):
\(x^2=1^2+1^2\)
\(x=\sqrt2\)
Atualmente, esse número é reconhecido como um número irracional e é resultado de muitos séculos de reformulações teóricas.
Algumas fontes históricas afirmam que, na época de Pitágoras, acreditava-se que a medida de todo segmento deveria ser sempre expressa por um número inteiro ou um número racional, o que também valeria para o exemplo que vimos acima, em que o segmento é a diagonal do quadrado.
No entanto, no exemplo anterior, não é isso que ocorre: temos a medida de um segmento expressa por um número irracional. Consequentemente, há suposições de que o teorema de Pitágoras contribuiu para um momento decisivo no desenvolvimento da Matemática, trazendo à tona uma verdadeira crise nas teorias conhecidas até então.
Contudo, estudos mais recentes questionam essa versão, argumentando que os números irracionais já eram conhecidos pelos egípcios e babilônios e que a contribuição dos matemáticos da Grécia Antiga foi desenvolver as bases teóricas sobre tais números (que seriam caracterizados de maneira ainda mais formal séculos depois).
Quem foi Pitágoras?
Pitágoras foi um filósofo grego nascido na ilha de Samos em torno de 570 a.C. Apesar das informações escassas sobre sua vida, esse pensador ficou conhecido por fundar a Escola Pitagórica, uma associação que estudava e relacionava aspectos filosóficos, matemáticos e religiosos. Para saber mais sobre sua vida e suas contribuições, acesse: Pitágoras.
Mapa Mental: Teorema de Pitágoras
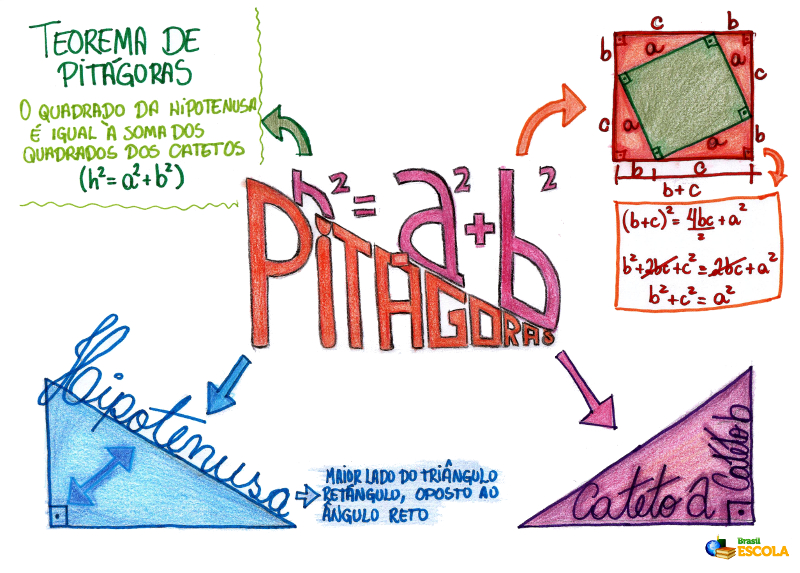
* Baixe o mapa mental sobre Teorema dee Pitágoras!
Exercícios resolvidos sobre teorema de Pitágoras
Questão 1
Em um triângulo retângulo isósceles, um dos catetos mede 8 cm. Qual a medida aproximada da hipotenusa?
A) 9,5 cm
B) 10,3 cm
C) 11,3 cm
D) 12,5 cm
E) 13,5 cm
Resolução
Alternativa C
Em um triângulo retângulo isósceles, os dois catetos possuem a mesma medida. Assim, temos um triângulo com dois catetos de medida 8 cm e uma hipotenusa de medida x. Portanto, podemos aplicar o teorema de Pitágoras:
\(x^2=8^2+8^2\)
\(x=\sqrt{128}\)
\(x≈11,3\)
Questão 2
Considere as afirmações abaixo sobre o teorema de Pitágoras.
I. O teorema de Pitágoras relaciona as medidas dos lados de qualquer triângulo.
II. O teorema de Pitágoras relaciona as medidas dos ângulos de um triângulo retângulo.
III. Dado um triângulo retângulo, se x é a medida da hipotenusa e as medidas dos catetos são y e z, então, pelo teorema de Pitágoras, \(x^2=y^2+z^2\).
É correto o que se diz em
A) I, apenas.
B) II, apenas.
C) III, apenas.
D) I e II.
E) I e III.
Resolução:
Alternativa C
I. O teorema de Pitágoras relaciona as medidas dos lados de qualquer triângulo. (falso)
O teorema de Pitágoras relaciona as medidas dos lados de um triângulo retângulo. Isso significa que esse teorema não é válido, por exemplo, para o triângulo equilátero.
II. O teorema de Pitágoras relaciona as medidas dos ângulos de um triângulo retângulo. (falso)
O teorema de Pitágoras não determina uma relação entre ângulos de um triângulo retângulo, mas sim entre lados de um triângulo retângulo.
III. Dado um triângulo retângulo, se x é a medida da hipotenusa e as medidas dos catetos são y e z, então, pelo teorema de Pitágoras, \(x^2=y^2+z^2\). (verdadeiro)
Fontes
IME UNICAMP. 5 demonstrações do Teorema de Pitágoras. Disponível em: http://www.ime.unicamp.br/~apmat/5-demonstracoes-do-teorema-de-pitagoras/.
GOLÇALVES, Carlos H.B.; POSSANI, Claudio. Revisitando a descoberta dos incomensuráveis na Grécia Antiga. Disponível em: https://rmu.sbm.org.br/wp-content/uploads/sites/27/2018/03/n47_Artigo02.pdf.
Por Maria Luiza Alves Rizzo
Professora de Matemática




