Círculo e circunferência

A circunferência e o círculo são figuras geométricas planas que aparecem com frequência na natureza. Assim como as outras formas geométricas possuem seus elementos, a circunferência e o círculo também possuem algumas características especiais.

Veja também: Ponto, reta, plano e espaço: conceitos básicos da geometria

Tópicos deste artigo

• 1 - O que é circunferência?
• 2 - Elementos da circunferência
  • Exemplo
• 3 - Perímetro da circunferência
  • Exemplo
• 4 - O que é o círculo?
• 5 - Elementos do círculo
• 6 - Área do círculo
  • Exemplo
• 7 - Exercícios resolvidos

O que é circunferência?

Uma circunferência é uma região do plano formada por pontos que são equidistantes de um ponto fixo chamado de centro da circunferência, ou seja, é formada por pontos que possuem a mesma distância do centro.

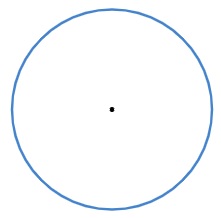
O ponto no meio da circunferência é o centro. Note que a distância entre todos os pontos em azul até o centro é a mesma.

Elementos da circunferência

Em toda circunferência, temos raio, diâmetro e corda. Vejamos agora cada um desses elementos:

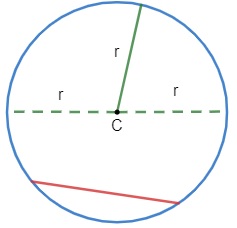
O raio (r) da circunferência é o segmento de reta que une o centro (C) da circunferência à sua extremidade (em azul). O segmento de reta que une as duas extremidades da circunferência e passa pelo centro C é chamado de diâmetro da circunferência e é denotado pela letra d. Observe que o diâmetro é a soma do raio da circunferência, logo:

d = r + r

d = 2·r

Como pode ser visto, o diâmetro é o dobro do raio. Qualquer outro segmento de reta que una dois extremos da circunferência e que não passe pelo centro é chamado de corda.

• Exemplo

Determine o raio de uma circunferência que possui diâmetro igual a 20 cm.

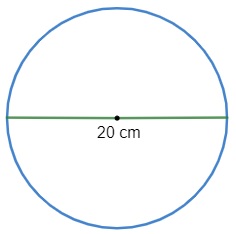
Como o diâmetro é duas vezes o raio, temos:

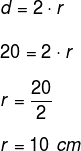
Em outras palavras, o raio é a metade do diâmetro.

Perímetro da circunferência

O perímetro da circunferência, também chamado de comprimento da circunferência, será representado por C. Imagine realizar um corte em um ponto qualquer da circunferência e “esticá-la” até que seja encontrado um segmento de reta. O que vamos realizar agora é determinar o tamanho desse segmento de reta.

O matemático e filósofo grego Arquimedes, em um de seus estudos, percebeu que a razão entre o comprimento da circunferência ( C ) e o diâmetro (d) sempre resultava em um mesmo número. Essa constante foi chamada de pi, que é denotado pelo símbolo π.

Dessa razão entre o comprimento de circunferência e o diâmetro, podemos encontrar uma expressão que possibilita determinar o comprimento da circunferência ou perímetro em função do raio. Veja:

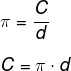
Sabemos que o diâmetro da circunferência é o dobro do raio, ou seja, d = 2r. Substituindo esse valor na expressão acima, teremos que o comprimento da circunferência em função da medida do raio é:

C = π · 2r

C = 2πr

Usualmente, utilizamos o valor de pi como sendo 3,14.

• Exemplo

Determine o comprimento de uma circunferência de raio 25 cm.

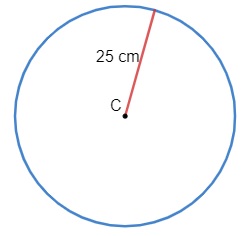
Substituindo o valor do raio na fórmula, temos:

C = 2πr

C = 2(3,14)(25)

C = 157 cm

O que é o círculo?

A definição de círculo é decorrente da definição de circunferência, pois um círculo é a região interna da circunferência. Fazendo um comparativo, temos que a circunferência é a extremidade, e o círculo é toda a região delimitada por essa extremidade. Veja a figura:

Leia támbém: Ângulos no círculo: como encontrá-los?

Elementos do círculo

• Como o círculo é uma região do plano determinada por uma circunferência, os elementos do círculo coincidem com os elementos da circunferência, isto é, ele também apresenta raio, diâmetro e corda. Veja:

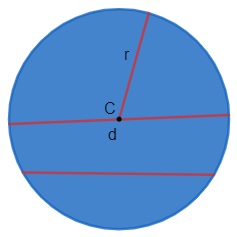
Área do círculo

A área do círculo é a medida de toda região delimitada pela circunferência. Considere um círculo de raio r:

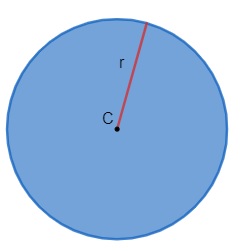
A área do círculo é dada por:

• Exemplo

Um círculo possui raio igual a 5 cm. Determine sua área.

Resolução:

Substituindo o valor do raio na fórmula, temos:

A = π r²

A = (3,14) 5²

A = 3,14 · 25

A = 78,5 cm²

Veja também: Comprimento da circunferência e área do círculo

Exercícios resolvidos

Questão 1 – Uma circunferência possui perímetro igual a 628 cm. Determine o diâmetro dessa circunferência e adote π = 3,14.

Solução

Como o perímetro é igual a 628 cm, podemos substituir esse valor na expressão de comprimento da circunferência.

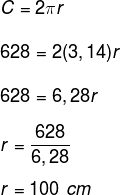
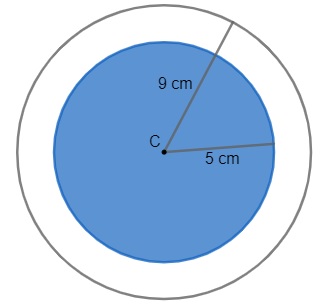
Questão 2 – Duas circunferências são concêntricas se elas possuem o mesmo centro. Sabendo disso, determine a área da figura em branco.

Solução:

Para determinar a área em branco, devemos calcular a área do círculo maior e subtrair a área do círculo em azul.

A_MAIOR = π r²

A_MAIOR = (3,14) · (9)²

A_MAIOR = (3,14) · 81

A_MAIOR = 254,34 cm²

Vamos calcular agora a área do círculo em azul:

A_AZUL = π r²

A_AZUL = (3,14) · (5)²

A_AZUL = (3,14) · 25

A_AZUL = 78,5 cm²

Assim, a área em branco é a diferença entre a área maior e a área azul.

A_BRANCO = 254,34 – 78,5

A_BRANCO = 175,84 cm² 

 

Por Robson Luiz
Professor de Matemática