O que é circunferência?

Circunferências são figuras geométricas planas geralmente representadas por figuras “perfeitamente redondas”, mas a representação geométrica nada mais é do que a representação de uma fórmula algébrica.

Todas as figuras geométricas são definidas com base em pontos. Os pontos são objetos que não possuem definição alguma, não possuem dimensão, mas representam localizações na Geometria Analítica. A reta, por sua vez, é uma figura geométrica representada por uma linha reta e infinita. Contudo, sua definição é dada apenas como conjunto de pontos.

De modo parecido, circunferências são também definidas com base em conjuntos de pontos e suas representações geométricas baseiam-se nessas definições. A definição de circunferência é a seguinte:

Definição de circunferência: Circunferência é uma figura geométrica pertencente ao plano que é constituída pelo conjunto de todos os pontos igualmente distantes de um ponto fixo desse plano.

Em outras palavras, dado o ponto fixo O, um ponto A, pertencente à circunferência C, possui a mesma distância até O que um ponto B, também pertencente à circunferência C, independentemente de quais sejam os pontos A e B.

Essa distância do ponto A até o ponto O (ou do ponto B até o ponto O) é chamada de raio da circunferência e é indicada pela letra r. Já o ponto O é o ponto fixo mencionado na definição acima e é conhecido como centro da circunferência.

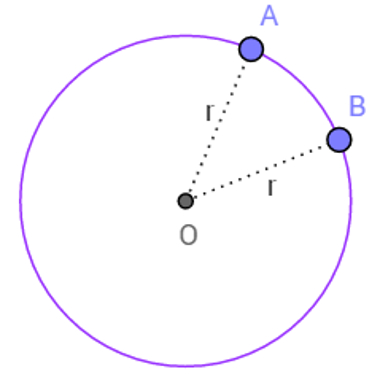
Centro O e pontos A e B equidistantes do ponto O, isto é, a distância de A e de B até O é igual a r Título: Exemplo de circunferência

Qualquer segmento de reta que ligue dois pontos pertencentes a uma circunferência é conhecido como corda. O segmento que ligar dois pontos pertencentes à circunferência e ainda possuir o centro dela será chamado de diâmetro. Em outras palavras, diâmetro é uma corda que “passa” pelo centro da circunferência. Com relação às propriedades, observam-se inicialmente duas em relação aos diâmetros: seu comprimento é igual a duas vezes o raio e não existe corda maior que um diâmetro em uma mesma circunferência.

Circunferência onde foram desenhadas cordas. Uma delas é o diâmetro

Dessa maneira, sendo r o raio e d o diâmetro, podemos escrever a seguinte relação entre o raio e o diâmetro de uma circunferência:

d = 2r

Por Luiz Paulo Moreira
Graduado em Matemática