PUBLICIDADE
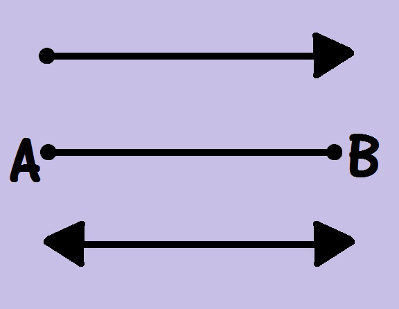
Um segmento de reta nada mais é do que uma parte de uma reta que possui um ponto inicial e um ponto final, chamados de “extremos”. Na figura a seguir temos uma reta r, e a parte vermelha compreendida entre os pontos A e B é um segmento de reta.
Observe o segmento de reta compreendido entre os pontos A e B
Nós podemos representar um segmento de reta através de duas letras que caracterizam os pontos de seus extremos com uma linha por cima delas: 
ou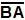 
. Eles devem ser lidos como “Segmento AB” ou “Segmento BA”. Se dois ou mais segmentos de retas possuem o mesmo comprimento, eles são chamados de congruentes.
De acordo com a sua posição, os segmentos de retas podem ser classificados ainda em segmentos consecutivos, segmentos colineares ou segmentos adjacentes. Se dois segmentos de retas forem paralelos, eles não serão classificados de acordo com nenhum desses três tipos de segmentos. Vejamos cada um deles:
Segmentos Consecutivos
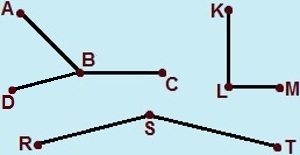
Dizemos que dois ou mais segmentos de retas são consecutivos quando eles possuem um ponto em comum. Observe os segmentos consecutivos na imagem a seguir:
.jpg)
Segmentos Colineares
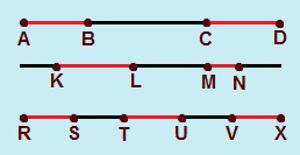
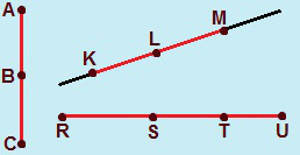
Dois ou mais segmentos de retas são ditos colineares quando por eles passa uma única reta ou quando pertencem a uma mesma reta. Um importante axioma da Geometria garante que, por dois pontos distintos, passa uma única reta. Podemos acrescentar que, por dois segmentos de retas colineares distintos, só é possível que uma única reta seja traçada. Veja alguns exemplos de segmentos colineares:
Segmentos Adjacentes
Se dois segmentos de retas forem consecutivos e colineares simultaneamente, isto é, se, além de terem pontos em comum, por eles passar uma única reta, eles serão segmentos de retas adjacentes. Podemos concluir que todos os segmentos adjacentes são, necessariamente, consecutivos e colineares. Vejamos alguns exemplos de segmentos adjacentes:
Por Amanda Gonçalves
Graduada em Matemática