O que é multiplicação?

A multiplicação é uma das quatro operações básicas da Matemática. Os números multiplicados são chamados de fatores da multiplicação, e o resultado é chamado de produto. Quando pelo menos um dos fatores é um número natural, podemos reconhecer a multiplicação como uma representação de adições consecutivas. Por exemplo, podemos escrever 2 + 2 + 2 como 3 × 2. 

Leia também: Potenciação — uma operação matemática que toma a multiplicação como base

Tópicos deste artigo

• 1 - Resumo sobre multiplicação
• 2 - Videoaula sobre multiplicação
• 3 - Termos da multiplicação
• 4 - Representação da multiplicação
• 5 - Como fazer a multiplicação?
  • → Multiplicação entre fatores inteiros de 1 a 10
  • → Multiplicação entre outros fatores
• 6 - Quais são as propriedades da multiplicação?
• 7 - Jogo de sinais
• 8 - Exercícios resolvidos sobre multiplicação

Resumo sobre multiplicação

• A multiplicação é uma das quatro operações básicas da Matemática.
• Em uma multiplicação, os elementos multiplicados são os fatores e o resultado é o produto.
• Se um dos fatores é um número natural, a multiplicação descreve adições sucessivas.
• Os principais símbolos para representar a operação de multiplicação são ⋅ e x.
• O algoritmo da multiplicação é a sequência de passos adotada para encontrar o produto entre dois números.
• As principais propriedades da multiplicação são: comutatividade, associatividade, elemento neutro, elemento nulo, inverso multiplicativo e distributividade.
• O jogo (ou regra) de sinais define o sinal de um produto a partir dos sinais dos fatores.

Videoaula sobre multiplicação

Termos da multiplicação

Em uma multiplicação, os elementos multiplicados são conhecidos como fatores e o resultado, como produto.

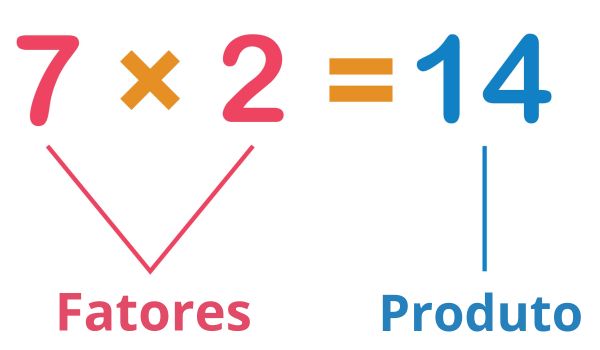
Vejamos um exemplo de como identificar esses elementos ao representar uma multiplicação a partir da adição de termos iguais.

• Exemplo:

Uma pessoa vai ao mercado e compra 5 pastas de dente, cada uma por R$ 1,50. Qual o valor total dessa compra?

Resolução:

Podemos escrever o valor total dessa compra utilizando a operação de adição:

\(R$\ 1,50\ +\ R$\ 1,50\ +R$\ 1,50+R$\ 1,50+R$\ 1,50\ =\ R$\ 7,50\)

Ou utilizando a operação de multiplicação:

\(5\ \times R$\ 1,50\ =\ R$\ 7,50\)

Lemos “5 vezes R$ 1,50 é igual a R$ 7,50.” Assim, o valor total da compra foi de R$ 7,50 (7 reais e 50 centavos). Nesse exemplo, os fatores são o número 5 e o valor R$ 1,50. Já o valor R$ 7,50 é o produto.

Importante: A multiplicação é a operação inversa da operação de divisão. Por exemplo, perceba que 4 ⋅ 5 = 20 e 20 ÷ 5 = 4.

Representação da multiplicação

Para representar a operação de multiplicação, utilizamos dois símbolos: ⋅ ou x. Veja:

7 × 10 ou 7 ⋅ 10

0,2 × 9 ou 0,2 ⋅ 9

Em alguns casos é mais indicado utilizar o símbolo ⋅ do que o símbolo x. Exemplo disso é quando estudamos expressões algébricas (como polinômios, equações e funções), nas quais a letra x possui outra finalidade. Veja:

\(3\cdot\left(x+\sqrt2\right)\)

\(\left(a+b\right)\cdot\left(x-y\right)\)

Quando um dos fatores é um elemento algébrico, a operação de multiplicação pode estar implícita, sem uso de nenhum símbolo. Veja:

\(10x\ =\ 10\ \cdot x\)

\(2ab\ =\ 2\cdot a\ \cdot b\)

Importante: Em algumas situações o asterisco (*) também é um símbolo adotado para representar a operação de multiplicação.

Como fazer a multiplicação?

→ Multiplicação entre fatores inteiros de 1 a 10

Se a multiplicação envolve fatores inteiros de 1 a 10, podemos consultar a tabuada:

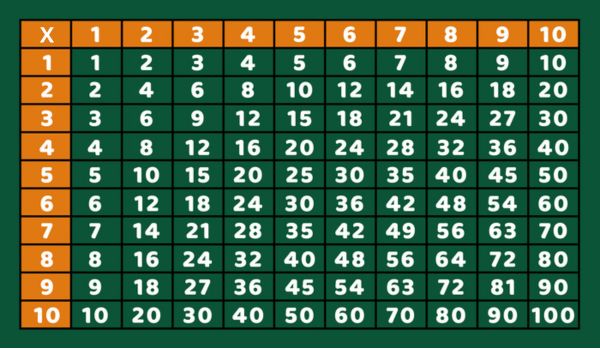
→ Multiplicação entre outros fatores

Caso os fatores sejam outros números, podemos construir uma sequência de passos para encontrar o resultado. Essa sequência de passos é chamada de algoritmo da multiplicação. Em resumo, o algoritmo da multiplicação determina que dados dois fatores, cada algarismo do segundo fator é multiplicado por cada algarismo do primeiro fator.

Mas cuidado: lembre-se de que a posição de um algarismo define seu significado. Assim, por exemplo, o número 25 (2 dezenas e 5 unidades) é diferente do número 52 (5 dezenas e 2 unidades), ainda que ambos sejam formados pelos algarismos 2 e 5.

Vejamos o funcionamento desse algoritmo através de dois exemplos.

• Exemplo 1:

Resolva a operação 431 ×5.

Resolução:

Passo 1 (montagem da multiplicação): Escreva um fator acima do outro, mantendo as ordens decimais alinhadas. Isso significa escrever a unidade do primeiro fator logo acima da unidade do segundo fator, a dezena do primeiro fator logo acima da dezena do segundo fator e assim por diante.

No exemplo, temos que o segundo fator possui apenas a ordem das unidades. Assim, a montagem dessa multiplicação é

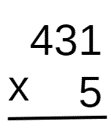
O resultado da multiplicação (ou seja, o produto) será indicado abaixo da linha horizontal.

Passo 2: Multiplique cada algarismo do segundo fator, começando pelas unidades, por cada algarismo do primeiro fator e escreva a resposta abaixo da linha horizontal, mantendo cada algarismo na ordem decimal adequada.

Primeiramente, vamos multiplicar a unidade do segundo fator pela unidade do primeiro fator. Como 5 ×1 = 5, escrevemos

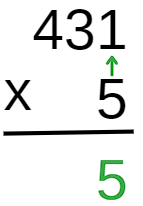
Agora, vamos multiplicar a unidade do segundo fator pela dezena do primeiro fator. Perceba que obtemos 5 ×3 = 15. Mas cuidado: o algarismo 3 no número 431 indica 3 dezenas, ou seja, 30. Assim, na realidade, estamos fazendo a multiplicação 5 ×30 =150. Por isso, o 5 (que representa 5 dezenas) é indicado na ordem das dezenas e o 1 (que representa 1 centena) é indicado acima da casa das centenas, para somar com o resultado que será trabalhado adiante.

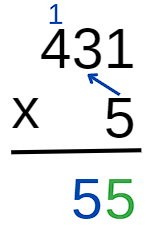
Por fim, vamos multiplicar a unidade do segundo fator pela centena do primeiro fator. Perceba que obtemos 5 ×4 = 20. Mais uma vez, devemos ter cuidado na interpretação: o 4 no número 431 indica 4 centenas, ou seja, 400. Na realidade, estamos calculando 5 ×400 = 2000. Além disso, o 1 acima do 4 indica que devemos acrescentar 1 centena. Portanto, obtemos o número 2100.

Note que não há outros algarismos no primeiro fator. Assim, encerramos o cálculo escrevendo o 1 na ordem das centenas e o 2 na ordem das unidades de milhar:

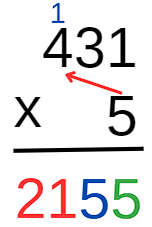
Isso significa que 431 ×5 = 2155.

• Exemplo 2:

Resolva a operação 12 ×34.

Resolução:

Passo 1: Monte a multiplicação.

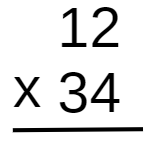
Passo 2: Multiplique cada algarismo do segundo fator, começando pelas unidades, por cada algarismo do primeiro fator e escreva a resposta abaixo da linha horizontal, mantendo cada algarismo na ordem decimal adequada.

Nesse exemplo, observe que o segundo fator possui dois algarismos. Devemos começar pelo algarismo das unidades e depois repetir o processo para o algarismo das dezenas, somando os resultados obtidos.

Primeiramente, multiplicamos a unidade do segundo fator por cada algarismo do primeiro fator.

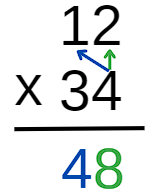
Antes de prosseguir, para manter cada algarismo na ordem decimal correta, devemos acrescentar um 0 na ordem das unidades, logo abaixo do 8. Isso ocorre porque o algarismo 3 no número 34 representa 3 dezenas (ou seja, 30). Lembre-se de que vamos repetir com o algarismo 3 do segundo fator o processo realizado com o algarismo 4 e somar os resultados.

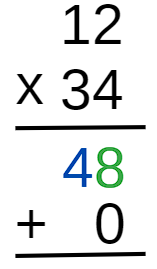
Agora, multiplicamos a dezena do segundo fator por cada algarismo do primeiro fator.

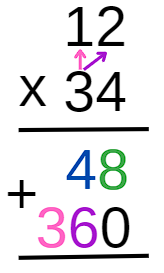
Por fim, somamos os resultados para obter o produto final.

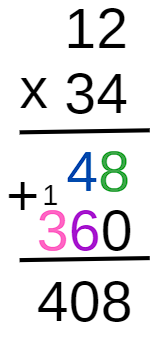
Isso significa que 12 ×34 = 408.

Quais são as propriedades da multiplicação?

A operação de multiplicação possui as seguintes propriedades:

• Comutatividade: a ordem dos fatores não altera o produto. Em outras palavras, se trocarmos a ordem dos elementos multiplicados, o resultado se mantém. Se a e b são números reais, temos que a ⋅b = b ⋅a. Veja o exemplo:

2 ×3 = 3 + 3 = 6

3 ×2 = 2 + 2 +2 = 6

• Associatividade: a ordem de associação para multiplicar três fatores não altera o produto. Se a, b e c são números reais, temos que \(\left(a\cdot b\right)\cdot c=a\cdot\left(b\cdot c\right)\). Veja o exemplo:

\(\left(5\cdot6\right)\cdot10=30\cdot10=300\)

\(5\cdot\left(6\cdot10\right)=5\cdot60=300\)

• Elemento neutro: o número 1 é o elemento neutro da multiplicação. Isso significa que todo elemento multiplicado por 1 resulta no próprio elemento. Se a é um número real não nulo (ou seja, a≠0), temos que \(\left(a\cdot b\right)\cdot c=a\cdot\left(b\cdot c\right)\). Veja os exemplos:

\(1\ \cdot4\ =\ 4\)

\(\left(-9\right)\cdot1=\left(-9\right)\)

• Elemento nulo: o número 0 é o elemento que anula a multiplicação. Em outras palavras, todo elemento multiplicado por 0 resulta em 0. Se a é um número real, temos que a ⋅0= 0 ⋅a=0. Veja os exemplos:

\(124\ \cdot0\ =\ 0\)

\(0\ \cdot1455\ =\ 0\)

Importante: Se o produto entre dois números reais é zero, então pelo menos um desses números é zero. Se a e b são números reais, temos que a⋅b=0⇒a=0 ou b=0.

• Inverso multiplicativo: todo número real possui um inverso multiplicativo. O produto entre um número real e seu inverso multiplicativo é 1. Se a é um número real não nulo (ou seja, a≠0), temos que \(a\cdot\frac{1}{a}=1\), em que \(\frac{1}{a}\) é chamado de inverso multiplicativo de a. Veja os exemplos:

\(20\cdot\frac{1}{20}=1\)

\(-6\cdot\left(\frac{1}{-6}\right)=1\)

• Distributividade: a operação de multiplicação é distributiva em relação à operação de adição e à operação de subtração. Se a, b e c são números reais, temos que a⋅b+c=a⋅b + a⋅c e a⋅b-c=a⋅b -a⋅c. Veja os exemplos:

\(3\cdot\left(1+x\right)=3\cdot1\ +\ 3\cdot x\ =\ 3\ +\ 3x\)

\(x\cdot\left(x-7\right)=x\cdot x-x\cdot7=x^2-7x\)

Importante: Note que podemos utilizar a propriedade distributiva para descrever o funcionamento do algoritmo da multiplicação. A partir do exemplo 1, podemos escrever \(431\times5=\left(400+30+1\right)\times5\). Aplicando a propriedade distributiva, temos que \(\left(400+30+1\right)\times5\ =\ 2000\ +\ 150\ +\ 5\ =\ 2155\).  Já a partir do exemplo 2, podemos escrever \(12\times34=12\times\left(30+4\right)\). Aplicando a propriedade distributiva, temos que \(12\times\left(30+4\right)=360+48=408\).

Jogo de sinais

O jogo (ou regra) de sinais determina o sinal do produto de uma multiplicação entre dois elementos a partir dos sinais dos fatores. O quadro abaixo apresenta essa regra:

Podemos resumir a regra de sinais da seguinte maneira:

• Dois fatores de mesmo sinal resultam em um produto de sinal positivo. Exemplo: \( \left(-8\right)\cdot\left(-9\right)=72\)
• Dois fatores de sinais diferentes resultam em um produto de sinal negativo. Exemplo: \( 11\cdot\left(-5\right)=-55\)

Veja também: Mínimo múltiplo comum (MMC) — o menor número múltiplo de dois ou mais números

Exercícios resolvidos sobre multiplicação

Questão 1

(Enem) Uma instituição de ensino superior ofereceu vagas em um processo seletivo de acesso a seus cursos. Finalizadas as inscrições, foi divulgada a relação do número de candidatos por vaga em cada um dos cursos oferecidos. Esses dados são apresentados no quadro.

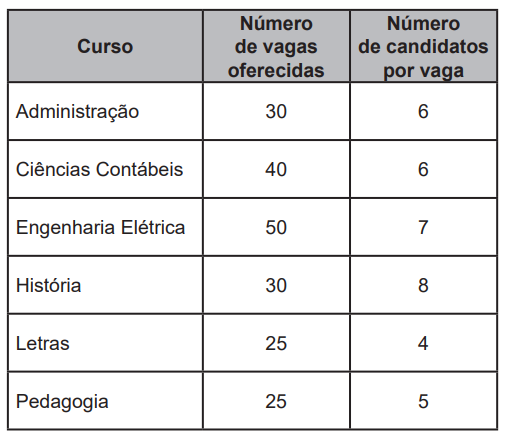
Qual foi o número total de candidatos inscritos nesse processo seletivo?

A) 200

B) 400

C) 1200

D) 1235

E) 7200

Resolução:

Alternativa D.

O número de candidatos inscritos por curso é o produto entre o número de vagas oferecidas e o número de candidatos por vaga:

Administração: 30 ⋅ 6 = 180 candidatos

Ciências Contábeis: 40 ⋅ 6 = 240 candidatos

Engenharia Elétrica: 50 ⋅ 7 = 350 candidatos

História: 30 ⋅ 8 = 240 candidatos

Letras: 25 ⋅ 4 = 100 candidatos

Pedagogia: 25 ⋅ 5 = 125 candidatos

Assim, o número total de candidatos inscritos nesse processo seletivo é igual a

180 + 240 + 350 + 240 + 100 + 125 = 1235

Questão 2

(Enem) Uma pessoa precisa contratar um operário para fazer um serviço em sua casa. Para isso, ela postou um anúncio em uma rede social. Cinco pessoas responderam informando preços por hora trabalhada, gasto diário com transporte e tempo necessário para conclusão do serviço, conforme valores apresentados no quadro.

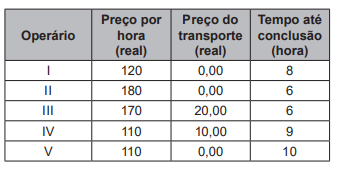
Se a pessoa pretende gastar o mínimo possível com essa contratação, irá contratar o operário

A) I.

B) II.

C) III.

D) IV.

E) V.

Resolução:

Alternativa A.

O valor V, em reais, para a contratação é indicado pela seguinte expressão:

V = (Preço por hora × Tempo) + Preço transporte

Assim, os valores informados por cada operário são

V_I = (120 × 8) + 0 = R$ 960

V_II = (180 × 6) + 0 = R$ 1080

V_III = (170 × 6) + 20 = R$ 1040

V_IV = (110 × 9) + 10 = R$ 1000

V_V = (110 × 10) + 0 = R$ 1100

Portanto, para gastar o mínimo possível, a pessoa deve contratar o operário I.

Crédito de imagem

[1] Patrick Herzberg / Shutterstock

Por Maria Luiza Alves Rizzo
Professora de Matemática