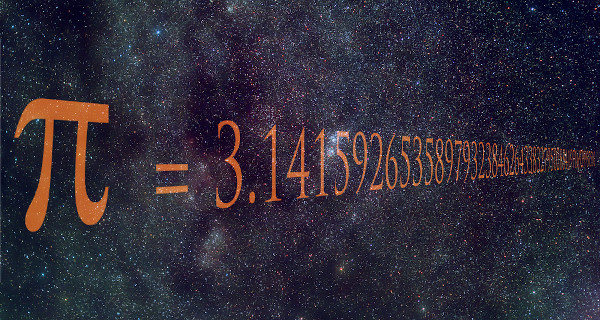Número pi (π)

O número pi, representado pela letra grega π, é uma das constantes mais conhecidas e mais importantes da Matemática. Como é um número irracional, ele é uma dízima não periódica e possui infinitas casas decimais, então é comum utilizarmos uma aproximação do valor de π para a resolução de problemas.

Esse número é uma constante, e o seu valor é de aproximadamente 3,141592653..., mas a aproximação mais utilizada para o valor de π é 3,14. O número π é utilizado em cálculos que envolvem formas circulares, como o cálculo do comprimento da circunferência, o cálculo da área do círculo e cálculos envolvendo esferas, cones e cilindros.

Leia também: Quando surgiram os números?

Tópicos deste artigo

• 1 - Resumo sobre o número pi (π)
• 2 - História do número pi (π)
• 3 - Qual o valor do número pi (π)?
• 4 - Como calcular o número pi (π)?
• 5 - Para que serve o pi (π)?

Resumo sobre o número pi (π)

• O número π (lê-se: pi) é uma das constantes mais conhecidas na Matemática.

• É utilizado para calcular grandezas envolvendo formas circulares.

• É um número irracional, logo é uma dízima não periódica.

• O valor de π = 3,141592653...

• É bastante comum utilizarmos aproximações para o valor de π. A mais utilizada é \(\pi=3,14\).

História do número pi (π)

A constante π apareceu na vida dos nossos antepassados há muitos anos, pois muitos matemáticos tentaram encontrar seu valor com precisão. Historiadores relatam que a busca por aproximações para o valor de π começou com os egípcios e babilônicos.

Anos depois, com base nos estudos realizados por Euclides, o matemático grego Arquimedes conseguiu uma aproximação para o valor de π começando pelo cálculo do perímetro de um hexágono e observando o que aconteceria com esse perímetro aumentando o número de lados do polígono. Ao perceber que quanto maior o lado desse polígono, mais próximo da circunferência esse polígono chegava, Arquimedes encontrou o valor 3,142 como aproximação para o valor de π.

Outros matemáticos utilizaram o mesmo método, aumentando o lado dos polígonos, e então Ptolomeu conseguiu encontrar uma aproximação mais precisa, π  = 3,1416, utilizando um polígono de 720 lados. Também tivemos contribuições posteriores dos chineses, que encontraram o valor de π = 3,14159 com um polígono de 3072 lados.

Com o passar do tempo e com o desenvolvimento da tecnologia, muitos matemáticos se ocuparam de descobrir o máximo de casas decimais possíveis para esse número. Atualmente, é conhecido um total de 62,8 trilhões de casas decimais do número π. Esse é o recorde mundial reconhecido pelo Guinness Book calculado pela Universidade de Ciências Aplicadas de Grisons.

Leia também: Como é feito o cálculo de raízes não exatas?

Qual o valor do número pi (π)?

Sabemos, portanto, que π é uma dízima não periódica, que possui infinitas casas decimais. Em exercícios da escola e de vestibulares, utilizamos normalmente uma aproximação para seu valor, como 3 ou 3,1 ou 3,14. Entretanto, como vimos, π possui muitas casas decimais, então para fazer contas com precisão, os matemáticos utilizam mais delas.

Veja a seguir o valor de π considerando as 200 primeiras casas decimais:

\(\pi =\)

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912

Como calcular o número pi (π)?

A constante π foi encontrada quando tentava-se calcular a razão entre o comprimento da circunferência o seu diâmetro.

\(\pi=\frac{comprimento}{diâmetro}=\frac{C}{d}\)

Acontece que um círculo nunca havia sido medido com a precisão necessária, logo, ao fazer essa divisão, os povos perceberam que o valor do cálculo sempre se aproximava de uma constante. Isso acontece para qualquer circunferência, com qualquer raio.

Para que serve o pi (π)?

A constante π é utilizada para cálculos envolvendo corpos redondos, como a área de um círculo, o comprimento de uma circunferência, o volume e a área total de cones, cilindros e esferas. Quando realizamos cálculos com figuras planas e sólidos geométricos que possuem faces arredondadas, o número π é essencial.

Por exemplo:

A fórmula para calcular o comprimento de uma circunferência é:

\(C=2\pi r\)

A fórmula da área de uma circunferência é:

\(A=\pi r^2\)

Já a fórmula para calcular o volume da esfera é:

\(V=\frac{4}{3}\pi r^3\)

Sendo assim, somente com a constante π é possível ter precisão no valor de grandezas envolvendo figuras planas de forma circular e sólidos geométricos com faces circulares.

Por Raul Rodrigues de Oliveira
Professor de Matemática