Diagrama de Venn

O diagrama de Venn, também conhecido como diagrama de Venn-Euler, é uma maneira de representar graficamente um conjunto, para isso utilizamos uma linha fechada que não possui auto-intersecção e representamos os elementos do conjunto no interior dessa linha. A ideia do diagrama é facilitar o entendimento nas operações básicas de conjuntos, como: relação inclusão e pertinência, união e intersecção, diferença e conjunto complementar.

Leia também: Operações entre números inteiros: conheça as propriedades

Tópicos deste artigo

• 1 - Representações do diagrama de Venn
• 2 - Relação de pertinência
• 3 - Relação de inclusão
• 4 - Operações entre conjuntos
  • • União
  • • Intersecção
• 5 - Exercícios resolvidos sobre Diagrama de Venn

Representações do diagrama de Venn

Como apresentado, o diagrama de Venn consiste em uma linha fechada (que não se entrelaça) na qual “colocamos” os elementos do conjunto em questão, logo, podemos representar um ou vários conjuntos de maneira simultânea. Veja os exemplos:

• Conjunto único

Podemos representá-lo utilizando uma única linha fechada, por exemplo, vamos representar o conjunto A = {1, 3, 5, 7, 9}:

• Entre dois conjuntos

Devemos fazer dois gráficos como o da representação do conjunto único. Entretanto, das operações com conjuntos sabemos que: dado dois conjuntos, eles podem ter intersecção ou não. Caso os dois conjuntos não possuam intersecção, eles recebem o nome de conjuntos disjuntos.

Exemplo 1

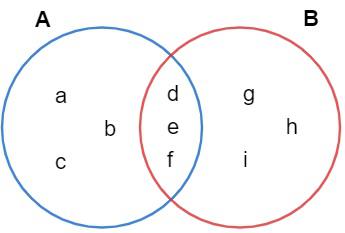
Represente, utilizando o diagrama de Venn, os conjuntos A = {a, b, c, d, e, f} e B = {d, e f, g, h, i}.

Observe que a intersecção é a parte do diagrama que pertence aos dois conjuntos, assim como na definição.

A ∩ B = {d, e, f}

Exemplo 2

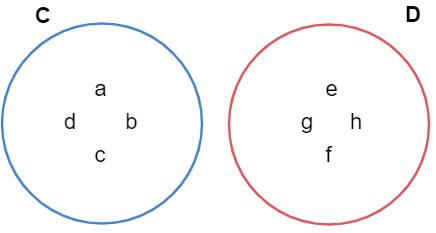
Represente os conjuntos C = {a, b, c, d}e D = {e, f, g, h}.

Observe que a intersecção desses conjuntos é vazia, pois não possui nenhum elemento que pertença simultaneamente a ambos, ou seja:

C ∩ D = { }

• Entre três conjuntos

A ideia por trás da representação utilizando o diagrama de Venn para três conjuntos é semelhante à da representação entre dois conjuntos. Nesse sentido, os conjuntos podem ser disjuntos um a um, isto é, não possuem nenhuma intersecção; ou podem ser disjuntos dois a dois, ou seja, somente dois deles possuem intersecção; ou todos possuem intersecção.

Exemplo

Representação, utilizando o diagrama de Venn, dos conjuntos A = {a, b, c, d}, B = {d, e, f, g} e C = {d, e, c, h}.

Veja também: Notações importantes sobre conjunto

Relação de pertinência

A relação de pertinência permite-nos dizer se um elemento pertence ou não a determinado conjunto. Para isso, utilizamos os símbolos:

Considere o conjunto A = {a, b, c, d}. Analisando-o, percebemos que g, por exemplo, não pertence a ele, assim, no diagrama de Venn, temos:

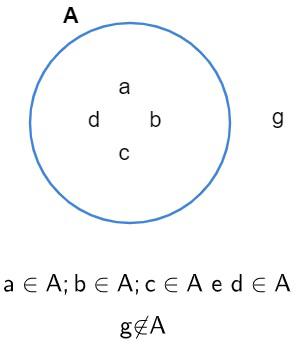
Relação de inclusão

A relação de inclusão permite-nos dizer se um conjunto está contido ou não em outro conjunto. Quando um conjunto está contido em outro, dizemos que se trata de um subconjunto. Para isso utilizamos os símbolos:

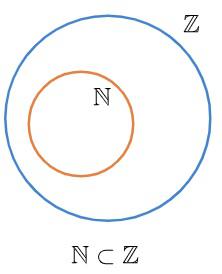
Um exemplo disso é a relação entre conjunto dos números naturais e conjunto dos números inteiros. Sabemos que o conjunto dos números naturais é subconjunto do conjunto dos números inteiros, isto é, o conjunto dos naturais está contido no conjunto dos inteiros.

Operações entre conjuntos

As operações básicas entre dois ou mais conjuntos são: união, intersecção e diferença entre dois conjuntos.

• União

A união entre dois conjuntos é formada pela junção dos elementos contidos em cada conjunto, em outras palavras: considera-se todos os elementos dos dois conjuntos. Veja:

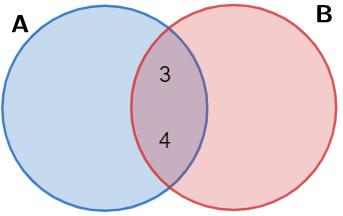
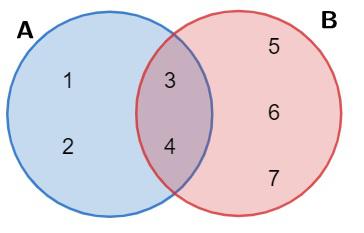
Considere os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5, 6, 7}. A união entre eles é dada por:

A U B = {1, 2, 3, 4, 5, 6, 7}
 

No diagrama de Venn, sombreamos a parte da união, isto é, ambos os conjuntos, confira:

• Intersecção

A intersecção é um novo conjunto numérico formado por elementos que pertencem, de maneira simultânea, a outros conjuntos. De modo geral, a intersecção entre conjuntos no diagrama de Venn é dada pela parte comum aos gráficos envolvidos. Veja:

Considerando novamente os conjuntos A = {1, 2, 3, 4} e B = {3, 4, 5, 6, 7}, temos que os elementos que pertencem ao conjunto A e ao conjunto B, simultaneamente, são:

A ∩ B = {3, 4}

• Diferença entre dois conjuntos

Considere dois conjuntos C e D, a diferença entre eles (C – D) será um novo conjunto formado por elementos que pertencem a C e não pertencem a D. De modo geral, podemos representar essa diferença, utilizando o diagrama de Venn, da seguinte maneira:

Exercícios resolvidos sobre Diagrama de Venn

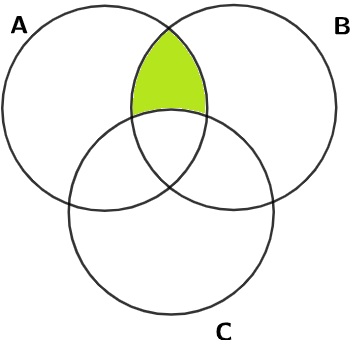
Questão 1 – (Ufal) Na figura a seguir, têm-se representados os conjuntos A, B e C não disjuntos. A região colorida representa o conjunto:

a) C – (A ∩ B)

b) (A ∩ B) – C

c) (A U B) – C

d) A U B U C

e) A ∩ B ∩ C

Solução

Alternativa b.

Lembrando das operações com conjuntos, sabemos que a intersecção entre dois conjuntos, no diagrama de Venn, é dada pela parte comum a eles. Considerando os conjuntos A, B e C e colorindo o conjunto intersecção A ∩ B, temos:

Título: Solução questão1 – parte 1

Observe que, se tirarmos os elementos do conjunto C, obtemos a parte colorida pedida pelo exercício, ou seja, devemos destacar a intersecção inicialmente e depois retirar os elementos de C.

(A ∩ B) – C

Questão 2 – (Uerj) Crianças de uma escola participaram de uma campanha de vacinação contra a paralisia infantil e o sarampo. Após a campanha, verificou-se que 80% das crianças receberam a vacina contra paralisia, 90% receberam a vacina contra o sarampo, e 5% não receberam nem uma nem outra.

Determine o percentual de crianças dessa escola que receberam as duas vacinas.

Solução

Como é desconhecido o percentual das crianças que tomaram as duas vacinas, vamos inicialmente chamá-lo de x. Lembre-se de que não devemos operar com o símbolo %, e sim escrevermos os percentuais do exercício em sua forma decimal ou fracionária.

80 % → 0,8

90% → 0,9

5% → 0,05

100% → 1

Para descobrirmos o total de crianças que tomaram somente a vacina contra paralisia, subtraímos a porcentagem verificada (80%) da porcentagem das que tomaram as duas (x), e o mesmo deve ser feito para as crianças que tomaram somente a vacina contra o sarampo. Assim:

Juntando todas as crianças, o percentual será de 100%, logo:

0,9 – x + x + 0,8 – x + 0,05 = 1

1,75 – x = 1

– x = 1 – 1,75

(–1) · – x = – 0,75 · (–1)

x = 0,75

x = 75%

Portanto, 75% das crianças da escola tomaram as duas vacinas.