Uma reta numérica é uma reta na qual são marcados e ordenados todos os números reais. Esses números são organizados sobre a reta para que todos os pontos nela representem um número real e de modo que nenhum ponto da reta represente dois números reais ao mesmo tempo.
Construindo uma reta numérica
A reta numérica é um objeto simples, e sua construção é fácil, entretanto, existem observações muito importantes a serem feitas sobre esse processo para a formalização do conceito de reta numérica e para ajudar a compreender seu uso. Para construir uma reta numérica, basta fazer o passo a passo a seguir:
1 – Em uma reta qualquer, marque um ponto que é chamado de origem, que está relacionado ao número 0 (zero).
2 – Escolha o sentido crescente da reta. Geralmente, os livros de Matemática ilustram retas numéricas na horizontal, com o sentido crescente para a direita. Isso significa que números à direita sempre serão maiores que números à esquerda.
Assim, considerando uma reta horizontal com origem já definida e sentido crescente à direta, por exemplo, o número 1 necessariamente estará à direita do zero e o número – 1 necessariamente estará à sua esquerda.
3 – Escolha uma unidade de medida mais adequada a essa reta numérica e assinale os números inteiros sobre ela. Essa unidade de medida será a distância entre dois números inteiros consecutivos. Portanto, se a unidade de medida escolhida for o centímetro, a distância entre o número – 1 e o número zero deve ser igual a 1 centímetro. Isso também pode ser usado para outras distâncias, por exemplo, a distância entre os números – 2 e 2 é igual a 4 centímetros.
Feita essa construção, a reta numérica estará pronta para uso. Sobre ela pode ser marcado qualquer número real. Se esse número for um decimal, 2,34, por exemplo, sabemos que ele está localizado entre os números 2 e 3. O espaço entre 2 e 3 precisa ser dividido em 100 partes iguais. A localização do número 2,34 é exatamente sobre a 34° parte dessa divisão.
Formalização do conceito
Dada uma reta r qualquer, cada intervalo entre dois pontos pertencentes a ela é chamado de segmento de reta. Para cada um desses segmentos de reta, é atribuído um número real, chamado “comprimento do segmento de reta”. Esse número real é que permite estabelecer uma relação entre pontos da reta e os números reais.
Para estabelecer essa relação, todos os segmentos de reta devem partir da origem dessa reta. Assim, todo comprimento de segmento de reta poderá ser compreendido como a distância entre um ponto e a origem da reta.
Dado o ponto A, situado a uma distância x da origem, dizemos que a coordenada de A é x, que está no lado positivo da reta se x for positivo, e no lado negativo da reta se x for negativo.
Essa relação construída entre as retas e os números reais é chamada biunívoca. Ela é uma “função bijetora” que relaciona cada ponto da reta a um único número real. Como essa relação é bijetora, não existe nenhum ponto da reta relacionado a dois ou mais números reais, ou dois números reais relacionados a dois ou mais pontos da reta. Além disso, todos os pontos da reta estão relacionados a números reais e todos os números reais estão relacionados a pontos da reta.
Em outras palavras, não existe um ponto da reta que não esteja relacionado a um número real e vice-versa.
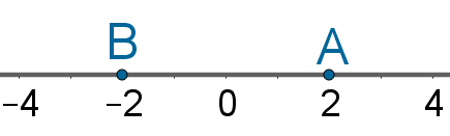
A imagem a seguir mostra o ponto A, cuja coordenada na reta numérica é x = 2, e o ponto B, cuja coordenada na mesma reta numérica é x = – 2.
Duas retas numéricas perpendiculares que se encontram em suas origens formam o plano cartesiano.
Por Luiz Paulo Moreira
Graduado em Matemática