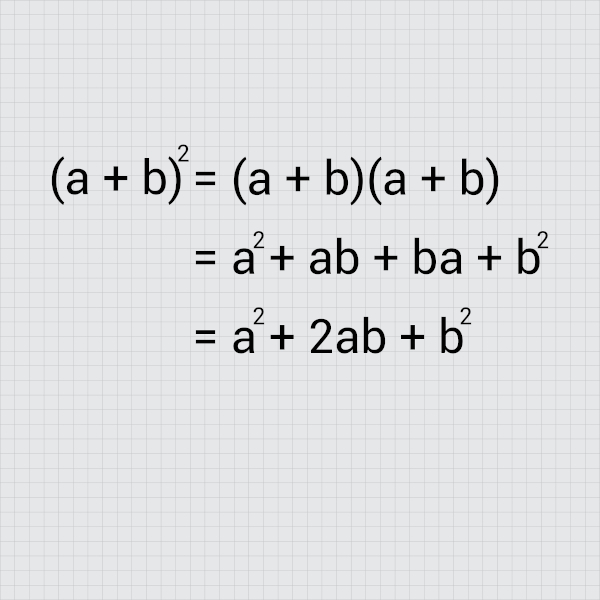Fatoração de polinômios

A fatoração de polinômios consiste em métodos desenvolvidos para reescrever um polinômio como um produto entre polinômios. Escrever o polinômio como a multiplicação entre dois ou mais fatores auxilia na simplificação de expressões algébricas e na compreensão de um polinômio.

Existem diferentes casos de fatoração, e para cada um deles há técnicas específicas. Os casos existentes são: fatoração por fator comum em evidência, fatoração por agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito, soma de dois cubos e diferença de dois cubos. 

Leia mais: O que é polinômio?

Tópicos deste artigo

• 1 - Resumo sobre fatoração de polinômios
• 2 - Casos de fatoração de polinômios
  • Fator comum em evidência
  • Agrupamento
  • Trinômio quadrado perfeito
  • Diferença de dois quadrados
  • Soma de dois cubos
  • Diferença de dois cubos
• 3 - Exercícios resolvidos sobre fatoração de polinômios

Resumo sobre fatoração de polinômios

• Fatoração de polinômios são técnicas utilizadas para representar o polinômio como um produto entre polinômios.

• Utilizamos essa fatoração para simplificação de expressões algébricas.

• Os casos de fatoração são:

  • Fatoração por fator comum em evidência;

  • Fatoração por agrupamento;

  • Trinômio quadrado perfeito;

  • Diferença de dois quadrados;

  • Soma de dois cubos;

  • Diferença de dois cubos.

Casos de fatoração de polinômios

Para realizar a fatoração de um polinômio, é necessário analisar em qual dos casos de fatoração a situação se enquadra, sendo eles: fatoração por fator comum em evidência, fatoração por agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito, soma de dois cubos e diferença de dois cubos. Vejamos como realizar a fatoração em cada um deles.

• Fator comum em evidência

Utilizamos esse método de fatoração quando há um fator comum a todos os termos do polinômio. Esse fator comum será colocado em evidência como um fator, e o outro fator, resultado da divisão dos termos por esse fator comum, será colocado dentro dos parênteses.

Exemplo 1: 

20xy + 12x² + 8xy²

Analisando cada termo desse polinômio, é possível perceber que x se repete em todos os termos. Além disso, todos os coeficientes (20, 12, e 8) são múltiplos de 4, logo, o fator comum a todos os termos é 4x.

Dividindo cada termo pelo fator comum, temos:

20xy : 4x = 5y

12x² : 4x = 3x

8xy² : 4x = 2y²

Agora, escreveremos a fatoração colocando o fator comum em evidência e a soma dos resultados encontrados entre parênteses:

4x (5y + 3x + 2y²)

Exemplo 2:

2a²b² + 3a³b – 4a⁵b³

Analisando a parte literal de cada termo, é possível perceber que a²b se repete em todos. Note que não há um número que seja divisor de 2, 3 e – 4 ao mesmo tempo. Logo, o fator comum será apenas a²b.

2a²b² : a²b = 2b

3a³b : a²b = 3a

4a⁵b³ : a²b = 4a³

Assim, a fatoração desse polinômio será:

a²b (2b + 3a + 4a³)

Veja também: Adição, subtração e multiplicação de polinômios — entenda como são feitas

• Agrupamento

Esse método é utilizado quando não há um fator comum a todos os termos do polinômio. Nesse caso, identificamos termos que podem ser agrupados possuindo fator comum e os colocamos em evidência.

Exemplo:

Fatore o seguinte polinômio:

ax + 4b + bx + 4a

Agruparemos os termos que possuem a e b como fator comum:

ax + 4a + bx + 4b

Colocando a e b em evidência nos termos de dois a dois, temos:

a(x + 4) + b(x + 4)

Note que dentro dos parênteses os fatores são os mesmos, então podemos reescrever esse polinômio como:

(a + b) (x + 4)

• Trinômio quadrado perfeito

Trinômios são polinômios com 3 termos. Um polinômio é conhecido como trinômio quadrado perfeito quando ele é resultado do quadrado da soma ou do quadrado da diferença, ou seja:

a² + 2ab + b² = (a + b)²

a² – 2ab + b² = (a – b)²

Importante: Nem sempre que houver três termos esse polinômio será um trinômio quadrado perfeito. Portanto, antes de realizar a fatoração, deve-se verificar se o trinômio se enquadra nesse caso.

Exemplo:

Fatore, se possível, o polinômio

x² + 10x + 25

Após analisar esse trinômio, extrairemos a raiz quadrada do primeiro e do último termo:

$\sqrt{x^2}=x$

$\sqrt{25}=5$

É importante verificar se o termo central, ou seja, 10x, é igual a $2\cdot\ x\cdot5$. Note que de fato é igual. Sendo assim, esse é um trinômio quadrado perfeito, que pode ser fatorado por:

x² + 10x + 25 = (x + 5)²

• Diferença de dois quadrados

Quando temos uma diferença de dois quadrados, podemos fatorar esse polinômio reescrevendo-o como o produto da soma pela diferença.

Exemplo: 

Fatore o polinômio:

4x² – 36y²

Primeiramente, calcularemos a raiz quadrada de cada um dos seus termos:

$\sqrt{4x^2}=2x$

$\sqrt{36y^2}=6y$

Agora, reescreveremos esse polinômio como o produto da soma pela diferença das raízes encontradas:

4x² – 36y² = (2x + 6y) (2x – 6y)

Leia também: Cálculo algébrico envolvendo monômios — saiba como ocorrem as quatro operações

• Soma de dois cubos

A soma de dois cubos, ou seja, a³ + b³, pode ser fatorada como:

a³ + b³ = (a + b) (a² – ab + b²)

Exemplo:

Faça a fatoração do polinômio:

x³ + 8

Sabemos que 8 = 2³, então:

x³ + 8 = (x + 2) (x² – 2x + 2²)

x³ + 8 = (x + 2) (x² – 2x + 4)

• Diferença de dois cubos

A diferença de dois cubos, ou seja, a³ – b³, não muito diferente da soma de dois cubos, pode ser fatorada como:

a³ – b³ = (a – b) (a² + ab + b²)

Exemplo:

Faça a fatoração do polinômio

8x³ – 27

Sabemos que:

8x³ = (2x)³

27 = 3³

Então temos que:

$8x^3-27=\left(2x-3\right)$

$8x^3-27=\left(2x-3\right)\left(4x^2+6x+9\right)$

Exercícios resolvidos sobre fatoração de polinômios

Questão 1

Utilizando a fatoração de polinômios para simplificar a expressão algébrica $\frac{x^2+4x+4}{x^2-4},$ , encontraremos:

A)  x + 2

B) x – 2

C) $\frac{x-2}{x+2}$

D) $\frac{x+2}{x-2}$

E) (x – 2) (x + 2)

Resolução:

Alternativa D

Analisando o numerador, observamos que x² + 4x + 4 é um caso de trinômio quadrado perfeito e pode ser reescrito como:

x² + 4x + 4 = (x + 2)²

Já o numerador x² – 4 é a diferença de dois quadrados e pode ser reescrito como:

x² – 4 = (x + 2) (x – 2)

Portanto:

$\frac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}$

Note que o termo x + 2 aparece tanto no numerador quando no denominador, então sua simplificação se dá por:

$\frac{x+2}{x-2}$

Questão 2

(Instituto Unifil) Considerando que dois números, x e y, são tais que x + y = 9 e x² – y² = 27, o valor de x é igual a:

A) 4

B) 5

C) 6

D) 7

Resolução:

Alternativa C

Note que x² – y² é a diferença entre dois quadrados e pode ser fatorada como o produto da soma pela diferença:

x² – y² = (x + y) ( x – y)

Sabemos que x + y = 9:

(x + y) (x – y) = 27

9 (x – y) = 27

x – y = 27 : 9

x – y = 3

Logo, podemos montar um sistema de equação:

$\begin{cases} x+y=9 & \quad\\ x-y=3 & \quad \end{cases}$

Realizando a soma das duas linhas:

 

2x + 0 y = 12

2x = 12

x = $\frac{12}{2}$

x = 6