Soma de dois cubos

Para entender a soma de dois cubos, é importante compreender que utilizamos o produto de dois polinômios para facilitar as operações e simplificações. No trabalho com polinômios, torna-se necessário conhecer a forma de fatorá-los, e encontrar a fatoração é buscar uma maneira de representar o polinômio como o produto de dois ou mais polinômios. Saber aplicar a fatoração desse polinômio é essencial para simplificar situações-problema que envolvam a soma de dois cubos. Existe uma fórmula utilizada para realizar essa fatoração.

Leia também: Como simplificar uma fração algébrica?

Tópicos deste artigo

• 1 - Como é feita a fatoração da soma de dois cubos?
• 2 - Fórmula da soma de dois cubos
• 3 - Exercícios resolvidos

Como é feita a fatoração da soma de dois cubos?

A fatoração de um polinômio é bastante comum na Matemática e seu objetivo é expressar esse polinômio como o produto de dois ou mais polinômios. A partir dessa representação, é possível realizar simplificações e resolver situações que envolvam, nesse caso, a soma de dois cubos. Para realizar a fatoração, é necessário conhecer a fórmula da soma de dois cubos.

Fórmula da soma de dois cubos

Considere a como o primeiro termo e b como o segundo termo e que eles podem ser qualquer número real, então temos que:

a³ + b³ = (a+b)(a² – ab +b²)

Analisando o segundo membro da equação, vamos mostrar que, ao aplicar a propriedade distributiva, podemos encontrar o primeiro membro.

(a+b)(a² – ab +b²) = a³ – a²b +ab² +a²b – ab² +b³

 Note que os termos em vermelho e os termos em azul são respectivamente opostos, logo sua soma é igual a zero, restando:

(a+b)(a² – ab +b²) = a³ + b³

Para realizar a fatoração do cubo da diferença, vamos aplicar a fórmula e encontrar os termos a e b, conforme o exemplo a seguir.

Exemplo 1:

Resolver x³ + 27.

Reescrevendo a equação, sabemos que 27=3³, então vamos representar por: x³ + 3³ → soma de dois cubos, em que x é o primeiro termo e 3 é o segundo termo.

Realizando a fatoração utilizando a fórmula, temos que:

x³ + 3³ = (x+3)(x² – x·3 +3²)

x³ + 3³ = (x+3)(x² – 3x +9)

Portanto, a fatoração de x³ + 27 é igual a (x+3)(x² – 3x +9).

Exemplo 2:

Resolver 8x³ + 125.

Reescrevendo a equação, sabemos que 8x³ = (2x)³ e que 125=5³, então vamos representar por: (2x)³ + 5³ → soma de dois cubos, em que 2x é o primeiro termo e 5 é o segundo termo.

Realizando a fatoração utilizando a fórmula, temos que:

(2x)³ + 5³ = (2x +5) ((2x)² – 2x·5+5²)

(2x)³ + 5³ = (2x+5) (4x² – 10x +25)

Portanto, a fatoração de 8x³ + 125 é igual a (2x+5)(4x² – 10x +25).

Veja também: Como somar e subtrair frações algébricas?

Exercícios resolvidos

Questão 1 – Sabendo que a³ + b³ = 1944 e que a+b = 1 e ab = 72, o valor de a²+b² é ?

A) 160

B) 180

C) 200

D) 240

E) 250

Resolução

Alternativa B.

Vamos fatorar a³ + b³.

a³ +b³ = (a+b) (a² – ab + b²)

Agora utilizaremos os dados da questão substituindo a+b, ab e a³ + b³:

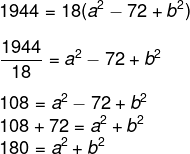
Questão 2 – A simplificação da expressão é:

A) 1

B) x+1

C) -3xy

D) x² + y²

E) 5

Resolução

Alternativa A.

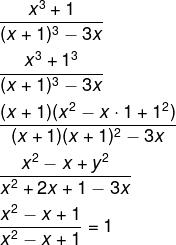
Por Raul Rodrigues de Oliveira
Professor de Matemática