O que é polinômio?

Polinômios são expressões algébricas formadas pela adição de monômios. Ambos são constituídos por números conhecidos e números desconhecidos. Antes de partirmos para as operações matemáticas que envolvem os polinômios, precisamos entender melhor alguns conceitos. Vamos lá?

→ O que são monômios?

Monômios são constituídos pelo produto entre números conhecidos e incógnitas (números desconhecidos comumente representados por letras). Divisões por incógnitas não são consideradas monômios, mas são chamados de frações algébricas.

Exemplos:

a) 4x

b) 7xy²

O número conhecido é chamado de coeficiente, e o restante do monômio é chamado de parte literal. Caso seja analisado dentro de um polinômio, o monômio também é chamado de termo. Um termo geralmente é reconhecido não por isso, mas por sempre ser separado por somas e subtrações. Quando a parte literal de dois ou mais monômios é igual, dizemos que eles são monômios semelhantes.

→ Exemplos de polinômios

Como dito anteriormente, qualquer expressão algébrica formada pela adição de monômios é chamada de polinômio. Dessa maneira, seguem os exemplos de polinômios:

a) 4xy + 2x + 7yw

b) 4x⁴ – x² + 60x – 7

→ Adição e subtração de polinômios

Reescreva os polinômios colocando termos semelhantes lado a lado. Some ou subtraia esses termos da mesma maneira que nos monômios. Veja um exemplo:

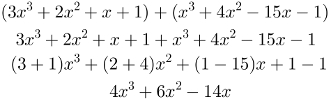
Já a subtração de polinômios envolve a propriedade distributiva da multiplicação e modifica todos os sinais do segundo polinômio. Somente depois de realizar esse jogo de sinais é que podemos continuar com a subtração. Observe:

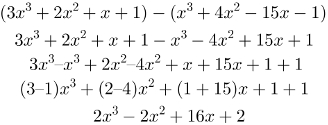
→ Multiplicação de polinômios

A multiplicação de polinômios é totalmente fundamentada na propriedade distributiva mais conhecida como chuveirinho. Para tanto, basta multiplicar cada monômio do primeiro polinômio por todos os monômios do segundo, observando os sinais dos resultados. Por exemplo:

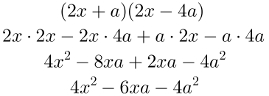
→ Divisão de polinômios

Para dividir dois polinômios, utilize o método chave, exatamente como é feito para números inteiros. Observe o exemplo:

Na divisão do polinômio P(x) = x³ + 7x² + 15x + 9 pelo polinômio D(x) = x + 1, P(x) é o dividendo, D(x) é o divisor e o resultado Q(x) é quociente e é obtido da seguinte maneira:

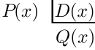
Primeiramente, procure um monômio que, multiplicado pelo termo de grau mais alto de D(x), tenha o termo de grau mais alto de P(x) como resultado. Esse monômio é x².

Encontrando-o, multiplique-o por D(x) e coloque o resultado sob P(x), exatamente como se faz na divisão de números inteiros. Observe:

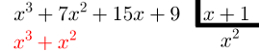
Lembre-se de que esse resultado deve ser subtraído de P(x), por isso, os sinais do resultado da multiplicação anterior devem ser trocados.

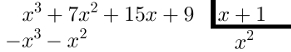
Feito isso, realize a subtração e “desça” todos os termos que não forem subtraídos:

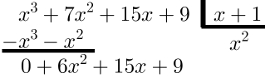
Repita o procedimento até que o resto possua grau menor que D(x).

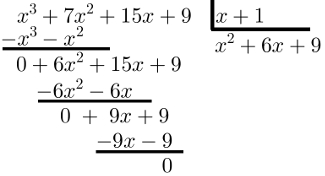
Por Luiz Paulo Moreira
Graduado em Matemática