Diferença de dois quadrados

Diferença de dois quadrados é o 5º caso de fatoração. Para compreendermos melhor como e quando utilizarmos é necessário que saibamos que diferença na matemática é o mesmo que subtração e que quadrado é elevar um número, letra ou termos ao quadrado.

A fatoração pela diferença de dois quadrados só poderá ser usada quando:

- Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios sejam quadrados.
- A operação entre eles for de subtração.

Veja alguns exemplos de expressões algébricas que seguem esse modelo:


• a² - 1, a expressão algébrica tem apenas dois monômios, os dois estão ao quadrado e entre eles há uma operação de subtração.
• 1 – a²
   3
• 4x² – y²

►Como escrever a forma fatorada dessas expressões algébricas.

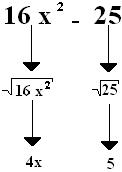
Dada a expressão algébrica 16x² – 25, veja os passos que devemos tomar para chegarmos a forma fatorada utilizando o 5º caso de fatoração.




A forma fatorada será (4x – 5) (4x + 5).

Veja alguns exemplos:

Exemplo 1:
A expressão algébrica x² – 64 é uma expressão com dois monômios e as raízes quadradas são respectivamente x e 8, então a sua forma fatorada é (x – 8) (x + 8).


Exemplo 2:
Dada a expressão algébrica 25x² – 81, a raiz dos termos 25x² e 81 é respectivamente 5x e 9. Então, a forma fatorada é (5x – 9) (5x + 9).

Exemplo 3:
Dada a expressão algébrica 4x² – 81y², a raiz dos termos 4x² e 81y² é respectivamente 2x e 9y. Então, a forma fatorada é (2x – 9y) (2x + 9y).

Por Danielle de Miranda
Graduação de Matemática