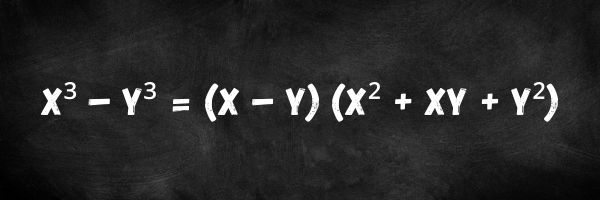A diferença de dois cubos é um caso particular de polinômios estudado na álgebra. Quando se obtém o cubo da diferença, é possível realizar a fatoração desse polinômio e reescrevê-lo como a multiplicação entre dois polinômios, o que pode auxiliar na simplificação de operações entre polinômios. Quando há a diferença entre dois cubos, é possível fatorar da seguinte maneira: x³ – y³ = (x – y) (x² + xy + y²).
Leia também: Fatoração de expressão algébrica — métodos práticos
Tópicos deste artigo
- 1 - Resumo sobre diferença de dois cubos
- 2 - O que é a diferença entre dois cubos?
- 3 - Fórmula da diferença de dois cubos
- 4 - Como é feita a diferença de dois cubos?
- 5 - Videoaula sobre fatoração de expressões algébricas
- 6 - Exercícios resolvidos sobre diferença de dois cubos
Resumo sobre diferença de dois cubos
- A diferença de dois cubos é um caso particular de fatoração de polinômios.
- Para fatorar a diferença entre dois cubos, utiliza-se a fórmula:
x³ – y³ = (x – y) (x² + xy + y²)
O que é a diferença entre dois cubos?
Na álgebra, o estudo dos polinômios possibilitou o desenvolvimento de seus casos de fatoração. Existem diversos casos de fatoração de polinômios, sendo que cada um deles é aplicado para determinada situação. A diferença entre dois cubos é, então, um caso particular de fatoração de polinômios, mas existem outros, como, por exemplo, o cubo da soma, a diferença de dois quadrados.
Fatorar um polinômio é reescrevê-lo como o produto entre dois ou mais fatores. Utilizam-se fatorações para simplificar operações envolvendo polinômios.
A diferença entre dois cubos nada mais é que a subtração entre dois monômios que podem ser reescritos como um termo elevado a cubo.
Exemplos:
-
x³ – y³
-
a³ – 1
-
8x³ – 27y³
-
64 – b³
Fórmula da diferença de dois cubos
Queremos reescrever a diferença entre dois cubos como a multiplicação de polinômios, ou seja, reescrevê-la na forma fatorada. Para isso, utilizamos a seguinte fórmula:
|
x³ – y³ = (x – y) (x² + xy + y²) |
x→ primeiro termo
y → segundo termo
-
Demonstração da fórmula da diferença de dois cubos
Se aplicarmos a propriedade distributiva na fatoração (x – y) (x² + xy + y²), encontraremos x³ – y³.
(x – y) (x² + xy + y²) = x³ + x²y + xy² – x²y – xy² – y³
(x – y) (x² + xy + y²) = x³ – y³
Dessa forma, podemos representar x³ – y³ como o produto (x – y) (x² + xy + y²), o que deixa demonstrada a fórmula de fatoração da diferença de dois cubos.
Leia também: Decomposição de um número em fatores primos
Como é feita a diferença de dois cubos?
Para realizar a fatoração da diferença entre dois cubos, é necessário conseguir identificar o valor do primeiro termo e do segundo termo. Para isso, é extraída a raiz cúbica desses números.
Exemplo 1:
Faça a fatoração do polinômio 64 – 8a³.
Resolução:
Primeiramente, extrairemos a raiz cúbica de cada termo para que seja possível identificar qual é o primeiro termo e qual é o segundo. Assim, calcula-se:
\(\sqrt{64}=4\)
\(\sqrt{8a^3}=2a\)
Então, temos que 4 é o primeiro termo e 2a , o segundo. Substituindo na fórmula:
\(\left(4^3-\left(2a\right)^3\right)=\left(4-2a\right)\left(4^2+4\cdot2a+\left(2a\right)^2\right)\)
Realizando o cálculo das potências e a multiplicação, encontraremos a forma fatorada do polinômio:
\(64-8a^3=\left(4-2a\right)\left(16+8a+4a^2\right)\)
Exemplo 2:
Fatore o seguinte polinômio:
\(\frac{125x^3}{27}-8y^3\)
Resolução:
Calculando a raiz cúbica de cada um dos termos, temos o seguinte:
\(\sqrt{\frac{125x^3}{27}}=\frac{5x}{3}\)
\(\sqrt{8y^3}=2y\)
Logo, conhecendo os primeiro e segundo termos, basta substituir na fórmula:
\(\left(\frac{5x}{3}\right)^3-\left(2y\right)^3=\left(\frac{5x}{3}-2y\right)\left(\left(\frac{5x}{3}\right)^2+\frac{5x}{3}\cdot2y+\left(2y\right)^2\right)\)
Agora, simplificando a expressão, encontraremos a forma fatorada do polinômio:
\(\frac{125x^3}{27}-{8y}^3=\left(\frac{5x}{3}-2y\right)\left(\frac{25x^2}{9}+\frac{10xy}{3}+4y^2\right)\)
Videoaula sobre fatoração de expressões algébricas
Leia também: Três erros comuns na simplificação de fração algébrica
Exercícios resolvidos sobre diferença de dois cubos
Questão 1
Existem dois números, b e a, consecutivos, cujo produto entre si é igual a 15500. O valor da expressão \(\frac{a^3-a^2-b^3-b^2}{31} \), sabendo que a > b, é:
A) 150
B) 500
C) 1500
D) 3100
E) 2500
Resolução:
Alternativa B
Utilizando a fatoração da diferença entre dois cubos, sabemos que:
\(a^3-b^3=\left(a-b\right)\ \left(a^2+ab+b^2\right)\)
Como esses números são consecutivos, sabemos que a > b, então \(a-\ b\ =\ 1.\ \)
Então, temos que:
\(a^3-b^3=1\cdot\left(a^2+15500+b^2\right)\)
\(a^3-b^3=a^2+15500+b^2\)
Isolando as incógnitas:
\(a^3-b^3-a^2-b^2=15500\)
Queremos o valor de:
\(\frac{a^3-a^2-b^3-b^2}{31}\)
Para isso, basta dividir 15500 por 31:
\(\frac{a^3-a^2-b^3-b^2}{31}=\frac{15500}{31}\)
\(\frac{a^3-a^2-b^3-b^2}{31}=500\)
Questão 2
Simplificando a expressão \( \frac{6x^3-6y^3}{2x^2+2xy+{2y}^2} \), encontraremos:
A) 3x + 2xy + 3y
B) 3(x – y)
C) 2x³ – 2y³
D) 2xy
E) x – y
Resolução:
Alternativa B
Fazendo a simplificação, obtém-se o seguinte:
\(\frac{6\left(x^3-y^3\right)}{2\left(x^2+xy+y^2\right)}\)
Podemos fazer a fatoração do numerador. Dessa forma, encontraremos:
\(\frac{6\left(x-y\right)\left(x^2+xy+y^2\right)}{2\left(x^2+xy+y^2\right)}\)
Note que há um fator comum, no numerador e no denominador. Logo, temos que:
\(\frac{6\left(x-y\right)}{2}\)
Sabemos que 6 : 2 = 3, então encontraremos a expressão algébrica 3x - y.
Por Raul Rodrigues de Oliveira
Professor de Matemática