A distância entre dois pontos é um dos conceitos mais importantes da Geometria Analítica. É por meio desse conceito que grande parte das definições e propriedades de figuras geométricas é construída.
A distância entre dois pontos é o menor segmento de reta que os liga. Sendo assim, o trabalho de encontrar uma distância resume-se a medir o comprimento de um segmento de reta.
Usualmente, na Geometria Analítica, as medidas de segmentos de reta são feitas por meio do Teorema de Pitágoras. Dessa maneira, esse mesmo teorema é usado para chegar a uma fórmula para o cálculo da distância entre dois pontos.
Demonstração da fórmula
Observe, na figura abaixo, os pontos A = (xA, yA, zA) e B = (xB, yB, zB). O primeiro passo é construir o menor segmento de reta que os liga. Para tanto, basta ligá-los com uma linha reta.
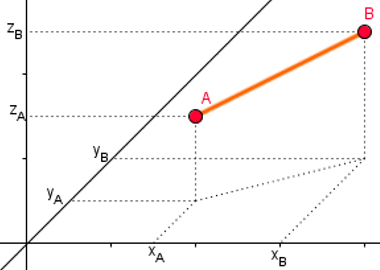
Feito isso, observe na figura abaixo o mesmo segmento visto de cima:
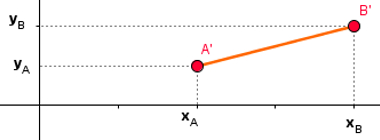
Observe que a vista superior reduz a primeira parte do problema à distância entre dois pontos no plano. Usaremos o Teorema de Pitágoras para descobrir o quadrado do comprimento do segmento A'B', projeção de AB sobre o plano xy. Lembre-se, contudo, de que os catetos a serem considerados possuem os tamanhos xB – xA e yB – yA.
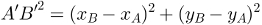
Feito isso, utilizaremos o Teorema de Pitágoras novamente para calcular o comprimento de AB. Observe que AB é a hipotenusa de um triângulo retângulo em que A'B' é cateto e base (esse segmento é paralelo à projeção do segmento AB e possui o mesmo tamanho) e zB – zA é o outro cateto e altura.
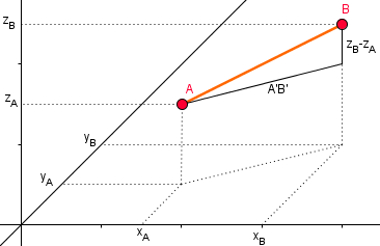
Desse modo, pelo teorema de Pitágoras, temos:
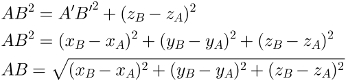
Assim finalizamos a demonstração, uma vez que foi encontrado o comprimento do segmento AB.
Fórmula da distância entre dois pontos no espaço
A partir dos cálculos acima, a distância entre dois pontos no espaço, denotada por dAB, fica definida da seguinte maneira:
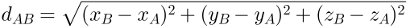
Para usar essa fórmula, basta substituir os valores numéricos das coordenadas dos pontos A e B e realizar os cálculos. Observe o exemplo:
Calcule a distância entres os pontos A = (0,2,2) e B = (-2, 0, 1):
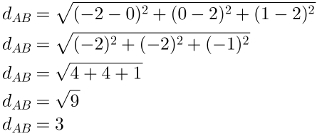
Por Luiz Paulo Moreira
Graduado em Matemática


