O princípio de Cavalieri foi desenvolvido na intenção de compreender melhor as medidas de volume. O cálculo de volumes nem sempre foi uma tarefa fácil, mas, com o princípio de Cavalieri, foi possível desenvolver fórmulas aplicáveis a vários sólidos geométricos a partir da comparação com o prisma ou cilindro.
Cavalieri percebeu que, dados dois sólidos com a mesma altura, se todas as secções paralelas ao plano em que esses sólidos estão apoiados formam figuras planas de área igual, então o volume desses sólidos é o mesmo.
Leia também: Quais as diferenças entre figuras planas e espaciais?
Tópicos deste artigo
- 1 - Definição do princípio de Cavalieri
- 2 - Volume do cilindro com o princípio de Cavalieri
- 3 - Volume da esfera com o princípio de Cavalieri
- 4 - Exercícios resolvidos
Definição do princípio de Cavalieri

Cavalieri foi um matemático que se dedicou ao estudo dos sólidos geométricos. Algo que o intrigava era o volume desses sólidos. Para calculá-lo, Cavalieri buscou comparar esses sólidos com outro sólido cujo volume já era conhecido. Com isso, ele percebeu que, por mais que o formato dos sólidos geométricos seja diferente, o volume deles é o mesmo, se a altura é a mesma e se para toda secção feita nos sólidos a área deles é a mesma.
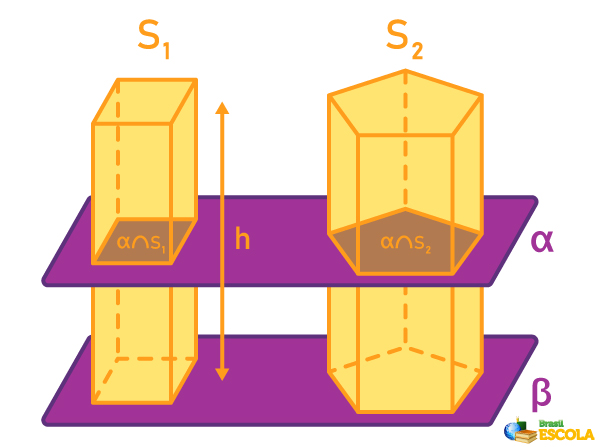
Na imagem, é possível perceber dois prismas com formatos diferentes e mesma altura. O primeiro deles é um prisma de base quadrada, e o outro é um prisma de base pentagonal. Ao realizar a secção desses sólidos com o plano α, é possível perceber que eles formam regiões com formatos diferentes. Porém, o princípio de Cavalieri diz que, se essas regiões sempre possuírem formato igual, então o volume desses sólidos geométricos também será o mesmo. A partir disso, é possível desenvolver a fórmula para o cálculo de volume de prismas.
V = Ab × h
O calculo da área da base depende diretamente do formato da base, logo é essencial o domínio do cálculo da área de polígonos para calcular o volume de prismas e de outros sólidos geométricos.
Volume do cilindro com o princípio de Cavalieri
Com base no princípio de Cavalieri, foi possível comparar o volume de prismas e cilindros. Sabemos que o volume de ambos é calculado pela seguinte fórmula:
A = Ab × h
Ab → área da base
h → altura
Quando a área da base e a altura de um prisma e a área da base e a altura do cilindro forem as mesmas, eles apresentarão também o mesmo volume, ainda que sejam sólidos geométricos com formatos diferentes.
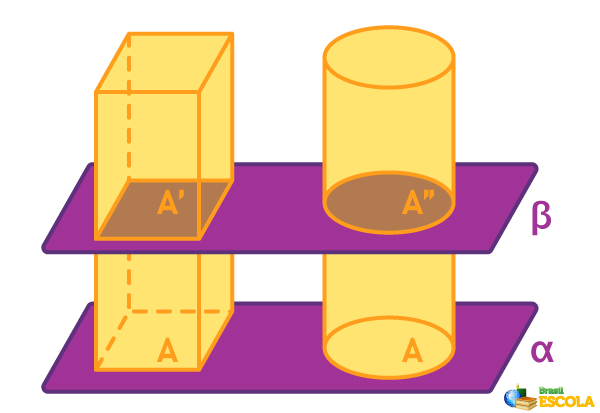
Como a base de um cilindro é igual a um círculo, a partir do princípio de Cavalieri, é possível deduzir a fórmula do volume do cilindro, pois a área do círculo é Ab = πr². Sendo assim, para calcular o volume do prisma, utilizamos a fórmula:
V = πr² × h
Leia também: Como calcular a área de sólidos geométricos?
Volume da esfera com o princípio de Cavalieri
Para deduzir a fórmula do volume da esfera, foi feita uma comparação do volume da esfera com o volume uma anticlépsidra, que é um sólido geométrico formado por um cilindro equilátero, ou seja, a altura é igual ao diâmetro da base, do qual subtraímos dois cones em que as bases coincidem com as bases do cilindro, conforme a imagem a seguir:
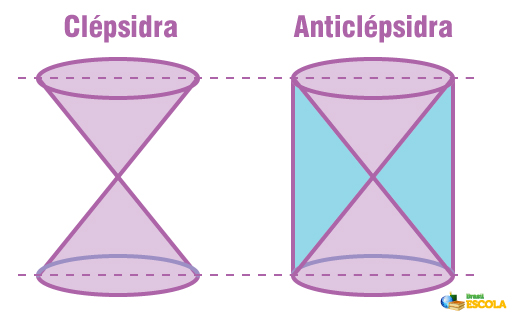
A anticlépsidra é a região em azul e o seu volume é igual ao volume do cilindro menos o volume dos dois cones. Como conhecemos o volume do cilindro e, sabendo que o volume do cone é 1/3 do volume do cilindro, podemos encontrar o volume da anticlépsidra.
V = Vcilindro – 2 Vcone
Sabemos que o volume do cilindro é:
Vcilindro = πr²·h
Como esse cilindro é equilátero, temos que h = 2r. Então, o volume do cilindro é:
Vcilindro = πr²·2r
Vcilindro = 2 πr³
Por outro lado, o volume do cone é igual a:
![]()
Como a altura é a metade da altura do cilindro, então a altura h é igual a r e, como são dois cones, temos que:
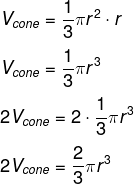
Assim sendo, o volume da anticlépsidra é igual a:
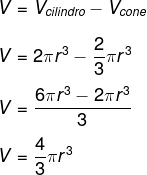
Conhecendo o volume da anticlépsidra, vamos compará-lo com o da esfera. Ao utilizarmos o princípio de Cavalieri, é possível perceber que a anticlépsidra possui a mesma altura da esfera, ou seja, h = 2r. Além disso, ao realizarmos secções nesses sólidos geométricos, é possível demonstrar que a área da circunferência formada na secção da esfera sempre será congruente à área da coroa formada na secção da anticlépsidra.
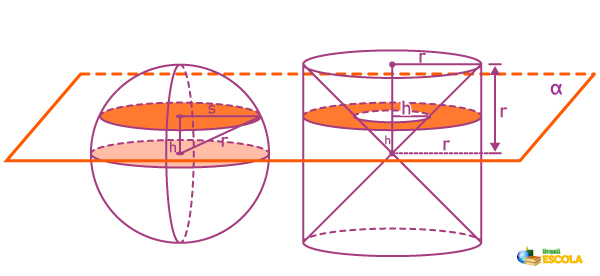
Para demonstrar que as áreas são iguais na esfera, sabemos que a área do círculo é:
Acírculo = πs²
Porém, no triângulo retângulo, temos que:
r² = h² + s²
s² = r² – h²
Logo, a área do círculo é igual a:
Acírculo = π( r² – h²)
Por outro lado, a área da coroa é a área da circunferência maior menos a área da circunferência menor, ou seja:
Acoroa = πr² - πh²
Acoroa = π (r² – h² )
Note que a área da coroa e do círculo são iguais, então, pelo princípio de Cavalieri, fica demonstrado que o volume da esfera é igual ao volume da anticlépsidra.
Veja também: Quais as diferenças entre circunferência e círculo?
Exercícios resolvidos
Questão 1 – (UEFS) O italiano Bonaventura Francesco Cavalieri (1589 – 1647), que foi discípulo de Gallileu, publicou, em 1635, sua Teoria do Indivisível, contendo o que hoje é conhecido como “princípio de Cavalieri”. Entretanto, sua teoria, que permitia que se encontrassem rapidamente com exatidão a área e o volume de muitas figuras geométricas, foi duramente criticada na época. Segundo seus críticos, a teoria não se mostrava suficientemente embasada. Em 1647, Cavalieri publicou a obra Exercitationes geometricae sex, na qual apresentou sua teoria de maneira mais clara. Esse livro transformou-se em fonte importante para os matemáticos do século XVII. (E CALCULO..., 2011).
De acordo com o princípio de Cavalieri, pode-se afirmar que, dados dois sólidos geométricos P1 e P2,
A) se esses sólidos possuem secções meridianas de mesma área, então P1 e P2 têm volumes iguais.
B) se esses sólidos possuem bases de mesma área e alturas de mesma medida, então P1 e P2 têm volumes iguais.
C) se esses sólidos possuem áreas laterais iguais e alturas de mesma medida, então os sólidosP1 e P2 têm volumes iguais.
D) se esses sólidos possuem áreas totais iguais e alturas de mesma medida, então P1 e P2 têm volumes iguais.
E) se um plano α, se qualquer plano β, paralelo a α, que intercepta um dos sólidos, também intercepta o outro e determina, nesses sólidos, secções de mesma área, então P1 e P2 têm volumes iguais.
Resolução
Alternativa E, pois é a única que descreve de forma correta o princípio de Cavalieri.
Questão 2 – (Enem 2014) Uma lata de tinta, com a forma de um paralelepípedo retangular reto, tem as dimensões, em centímetros, mostradas na figura.
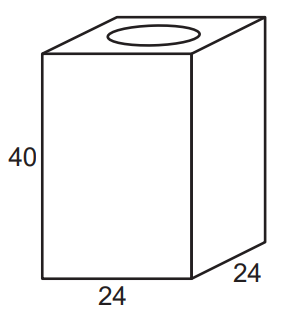
Será produzida uma nova lata, com o mesmo formato e volume, de tal modo que as dimensões de sua base sejam 25% maiores que as da lata atual. Para obter a altura da nova lata, a altura da lata atual deve ser reduzida em:
A) 14,4%.
B) 20,0%.
C) 32,0%.
D) 36,0%.
E) 64,0%.
Resolução
Alternativa D.
Sabemos que o volume da lata é igual ao produto das três dimensões:
V = 40 × 24 × 24
V = 23.040
Por outro lado, as dimensões da sua base vão sofrer um aumento de 25%, então multiplicaremos 24 por 1,25, para encontrar a nova medida.
24 × 1,25 = 30
Seja h a nova altura, então:
V = 30 × 30 × h = 23.040
900h = 23.040
h = 23.040/900
h= 25,6
Sabendo que a altura era de 40 e agora é de 25,6, então, ao realizar a divisão 25,6/40 = 0,64, isso corresponde a 64% do valor da altura anterior: 100% - 64 % = 36% de redução.
Por Raul Rodrigues de Oliveira
Professor de Matemática

