Distância entre dois pontos

A distância entre dois pontos é o primeiro conceito aprendido e um dos mais importantes dentro da geometria analítica, considerando que outros conceitos dessa área derivam da ideia de distância entre dois pontos.

Leia também: Condição de alinhamento de três pontos

Tópicos deste artigo

• 1 - O que é distância entre dois pontos?
• 2 - Distância entre dois pontos no plano cartesiano
• 3 - Fórmula da distância entre dois pontos
• 4 - Como calcular a distância entre dois pontos?
  • Exemplo
• 5 - Exercícios resolvidos

O que é distância entre dois pontos?

A distância entre dois pontos depende do lugar geométrico em que esses pontos estão localizados. Por exemplo, se dois pontos estão em uma reta, a distância é dada pelo módulo da diferença entre eles, veja:

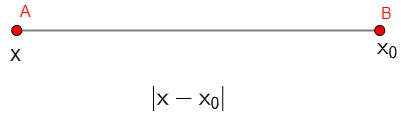
• Exemplo

Imagine a seguinte situação, em uma viagem, quando estamos passando por uma rodovia, temos algumas placas que marcam o quilômetro ou posição em que estamos naquele instante. Em um instante inicial passamos pela placa km 12, em seguida passamos pela placa km 68.

Para sabermos quanto andamos, é preciso considerar as duas placas: a do km 12 e a do km 68. Desse modo calculamos o módulo da diferença entre esses dois pontos para obtermos a distância percorrida, assim:

|12 - 68|=

|68 - 12| =

56 km

Distância entre dois pontos no plano cartesiano

Para determinar a distância entre dois pontos no plano cartesiano, é necessário realizar a análise tanto no sentido do eixo das abscissas (x) quanto no do eixo das ordenadas (y). Confira:

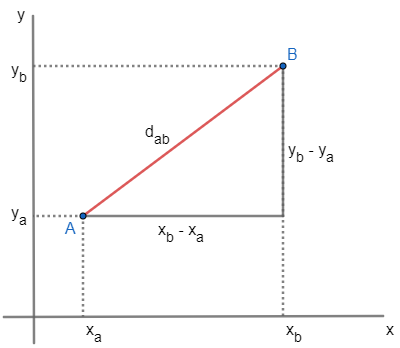
Note que na distância entre o ponto A e B existe uma variação tanto no eixo x quanto no eixo y, logo, a distância entre os pontos deve ser dada em função dessas variações.

Veja também que a distância entre os pontos é a hipotenusa do triângulo formado. Além disso, aplicando o teorema de Pitágoras e isolando o lado d_ab, temos:

Leia também: Generalidades sobre as equações da reta

Fórmula da distância entre dois pontos

A distância entre os pontos A(x_a, y_a) e B(x_b, y_b) é definida pelo comprimento do segmento representado por d_ab e tem medida dada por:

Como calcular a distância entre dois pontos?

Para determinar a distância entre dois pontos no plano, basta substituir corretamente os valores das coordenadas dos pontos na fórmula. Veja a seguir:

• Exemplo

Calcular a distância entre os pontos P (-3, -11) e Q (2, 1).

Perceba que na fórmula devemos subtrair os valores das abscissas de cada ponto e, em seguida, elevar ao quadrado, e o mesmo deve acontecer com os valores das ordenadas. Assim:

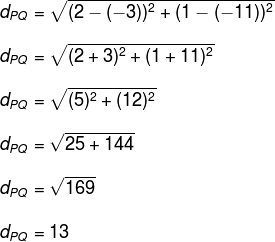
Exercícios resolvidos

Questão 1 – Sabendo que a distância entre os pontos A e B é de (raiz de 29) e que o ponto A (1, y_a) pertencente ao eixo O_x e B (-1, 5), determine y_a.

Solução:

Substituindo na fórmula de distância entre dois pontos, temos:

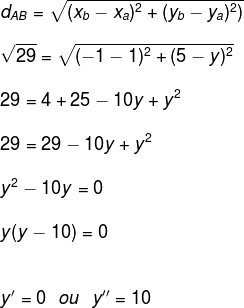
Como o ponto A pertence ao eixo X, então de fato y = 0.

Questão 2 – (UFRGS) A distância entre os pontos A (-2, y) e B (6, 7) é 10. O valor de y é:

a) -1

b) 0

c) 1 ou 13

d) -1 ou 10

e) 2 ou 12

Solução

Substituindo os dados do enunciado, temos:

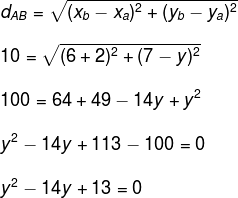
Resolvendo a equação do segundo grau, segue que:

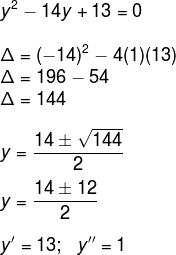
Resposta: Alternativa C 

Por Robson Luiz
Professor de Matemática