O que é trigonometria?

Trigonometria é uma palavra de origem grega que remete à medida de três ângulos. Os estudos dessa área da Matemática voltam-se para os triângulos, que são polígonos que possuem três lados e, consequentemente, três ângulos. Em um primeiro momento, a trigonometria ocupa-se de estudar algumas propriedades e relações dos triângulos retângulos para posteriormente relacionar as medidas dos lados dos triângulos com as medidas dos ângulos.

Essas propriedades e relações são expandidas para triângulos quaisquer por meio dos teoremas conhecidos como lei dos senos e lei dos cossenos. Posteriormente, alguns desses resultados são observados em triângulos cujos lados são segmentos notáveis de um círculo, que fica conhecido como “círculo trigonométrico”.

A trigonometria propõe uma grande novidade. Antes dela só era possível considerar cálculos e propriedades que envolvessem exclusivamente lados ou exclusivamente ângulos de um triângulo ou relações básicas entre esses elementos. Com a sua chegada, é possível relacionar diretamente as medidas de lados de um triângulo com a medida de um de seus ângulos. Vale ressaltar que as relações entre os lados e segmentos notáveis dentro de um triângulo também compõem a trigonometria.

Antes de aprofundar o conceito de trigonometria, é importante saber quais são os elementos mais importantes em um triângulo retângulo. Esses elementos estão expostos a seguir:

Elementos de um triângulo retângulo

Todo triângulo retângulo pode ser subdividido em outros dois triângulos retângulos, conforme a figura abaixo, traçando a altura “h” relativa à base “a”.

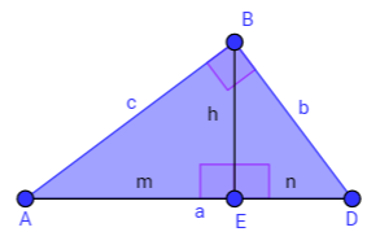
A altura desse triângulo retângulo forma dois ângulos de 90° com sua base

Considerando o triângulo ABD, retângulo em B, é possível observar os seguintes elementos:

1 – Os lados AB e BD são chamados de catetos e suas medidas são c e b, respectivamente;

2 – O lado AD é chamado de hipotenusa e sua medida é a. Esse lado sempre será oposto ao ângulo de 90°;

3 – BE é a altura do triângulo ABD relativa à base AD e sua medida é h. (lembrando que a altura sempre forma ângulo de 90° com a base relativa a ela);

4 – AE é a projeção ortogonal do cateto AB sobre a hipotenusa. Sua medida é m;

5 – ED é a projeção ortogonal do cateto BD sobre a hipotenusa. Sua medida é n.

A seguir, apresentamos e discutimos algumas propriedades vistas na trigonometria, tendo como base os elementos do triângulo retângulo expostos anteriormente.

Relações métricas no triângulo retângulo

São igualdades que relacionam lados, altura e projeções ortogonais de um triângulo retângulo:

1) c² = m·a

2) b·c = a·h

3) h² =m·n

4) b² = n·a

5) a² = b² + c² (teorema de Pitágoras)

Relações ou razões trigonométricas no triângulo retângulo

Essas igualdades relacionam razões entre os lados de um triângulo retângulo com um de seus ângulos agudos. Para tanto, é necessário fixar um dos dois ângulos e observar, no triângulo retângulo, as definições de cateto oposto e cateto adjacente:

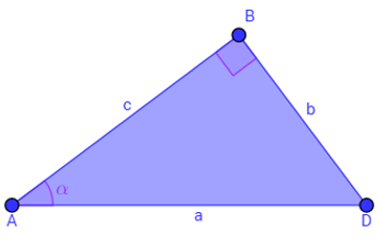
Triângulo retângulo, com destaque para o ângulo α

BD é o cateto oposto ao ângulo α;

AB é o cateto adjacente ao ângulo α.

Esses são os pré-requisitos para definir as razões trigonométricas. São elas:

→ Seno de α

sen α = Cateto oposto a α
           Hipotenusa

→ Cosseno de α

cos α = Cateto adjacente a α
             Hipotenusa

→ Tangente de α

tg α = Cateto oposto a α
          Cateto adjacente a α

Essas razões valem para qualquer triângulo retângulo que possua um ângulo agudo igual a α. O resultado dessas divisões sempre é o mesmo, independentemente do comprimento do lado do triângulo, pois dois triângulos que possuem dois ângulos iguais, em virtude da semelhança de triângulos ângulo-ângulo, têm lados proporcionais. Daí segue que a razão entre os lados é igual.

Círculo trigonométrico

Também chamado de ciclo trigonométrico ou circunferência trigonométrica (nomes mais corretos, mas menos usuais), trata-se de uma circunferência orientada de raio 1. Nessa circunferência, é construído um triângulo retângulo, cujo ângulo α coincide com a origem, de modo que a altura desse triângulo vai do eixo das abcissas até a borda do círculo.

Essa altura coincide com o valor de seno, por ser o cateto oposto ao ângulo α. Já a medida que vai do ponto de encontro da altura com o eixo das abcissas até a origem coincide com o cateto adjacente ao ângulo α, isto é, com o valor do cosseno.

Essas coincidências ocorrem porque a hipotenusa é sempre 1, pois ela é o raio do círculo. Observe essas propriedades na imagem abaixo:

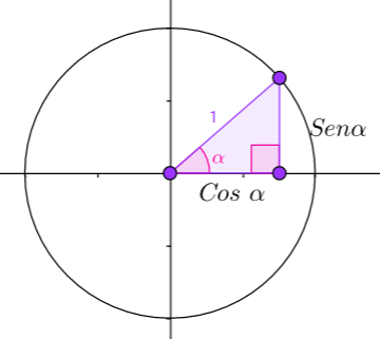
Círculo de raio 1, no qual é colocado um triângulo retângulo para avaliar suas propriedades

Qualquer que seja o triângulo retângulo construído nesse círculo, o cateto que coincide com uma parte do eixo das abcissas mede exatamente o valor do cosseno de α e o outro cateto mede exatamente seno de α.

Funções trigonométricas

Utilizando o círculo trigonométrico, é possível definir funções trigonométricas que relacionam cada elemento do conjunto dos números reais a um único elemento também do conjunto dos números reais. Contudo, esses números são expressos em radianos, que é uma unidade de medida em função de π utilizada porque, após 360° no círculo trigonométrico, a contagem de graus e, consequentemente, dos elementos do domínio e contradomínio de uma função com base nele pode ser reiniciada do zero.

Relações fundamentais

As relações fundamentais da trigonometria são:

1) Relação fundamental 1

Sen²α + cos²α = 1

2) Tangente de α

tg α = sen α
         cos α

3) Cotangente de α, que é o inverso da tangente de α

cotg α = cos α
             sen α

4) Secante de α, que é o inverso do cosseno de α

sec α = 1
             cos α

5) Cossecante de α, que é o inverso do seno de α

cossec α = 1
                 sen α

6) Relação decorrente 1

tg²α + 1 = sec²α

7) Relação decorrente 2

cotg²α + 1 = cossec²α

8) Relação recorrente 3

cotg α = 1
            tg α

Por Luiz Paulo Moreira
Graduado em Matemática