As relações métricas são equações que relacionam as medidas dos lados e de alguns outros segmentos de um triângulo retângulo. Para definir essas relações, é importante conhecer esses segmentos.
Elementos do triângulo retângulo
A figura a seguir é um triângulo retângulo ABC, cujo ângulo reto é Â e é cortado pela altura AD:
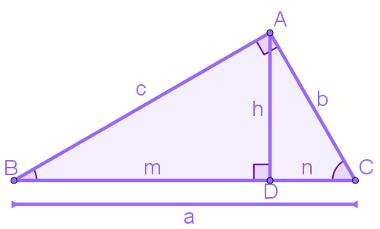
Nesse triângulo, observe que:
-
A letra a é a medida da hipotenusa;
-
As letras b e c são as medidas dos catetos;
-
A letra h é a medida da altura do triângulo retângulo;
Não pare agora... Tem mais depois da publicidade ;) -
A letra n é a projeção do cateto AC sobre a hipotenusa;
-
A letra m é a projeção do cateto BA sobre a hipotenusa.
Teorema de Pitágoras: primeira relação métrica
O teorema de Pitágoras é o seguinte: o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Ele é válido para todos os triângulos retângulos e pode ser escrito da seguinte maneira:
a2 = b2 + c2
*a é hipotenusa, b e c são catetos.
Exemplo:
Qual é a medida da diagonal de um retângulo cujo lado maior mede 20 cm e o lado menor mede 10 cm?
Solução:
A diagonal de um retângulo divide-o em dois triângulos retângulos. Essa diagonal fica sendo a hipotenusa, como mostra a figura a seguir:
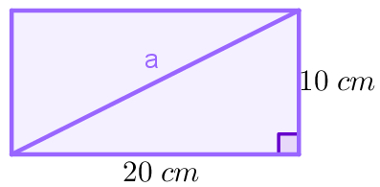
Para calcular a medida dessa diagonal, basta usar o teorema de Pitágoras:
a2 = b2 + c2
a2 = 202 + 102
a2 = 400 + 100
a2 = 500
a = √500
a = 22,36 cm, aproximadamente.
Segunda relação métrica
A hipotenusa do triângulo retângulo é igual à soma das projeções de seus catetos sobre a hipotenusa, ou seja:
a = m + n
Terceira relação métrica
O quadrado da hipotenusa de um triângulo retângulo é igual ao produto das projeções de seus catetos sobre a hipotenusa. Matematicamente:
h2 = m·n
Assim, se for necessário descobrir a medida da hipotenusa conhecendo apenas as medidas das projeções, poderemos usar essa relação métrica.
Exemplo:
Um triângulo cujas projeções dos catetos sobre a hipotenusa medem 10 e 40 centímetros tem que altura?
h2 = m·n
h2 = 10·40
h2 = 400
h = √400
h = 20 centímetros.
Quarta relação métrica
É usada para descobrir a medida de um cateto quando as medidas de sua projeção sobre a hipotenusa e a própria hipotenusa são conhecidas:
c2 = an
e
b2 = an
Perceba que b é a medida do cateto AC, e n é a medida de sua projeção sobre a hipotenusa. O mesmo vale para c.
Exemplo:
Sabendo que a hipotenusa de um triângulo retângulo mede 16 centímetros e que uma de suas projeções mede 4 centímetros, calcule a medida do cateto adjacente a essa projeção.
Solução:
O cateto adjacente a uma projeção pode ser encontrado a partir de qualquer uma dessas relações métricas: c2 = am ou b2 = an, pois o exemplo não especifica o cateto em questão. Assim:
c2 = a·m
c2 = 16·4
c2 = 64
c = √64
c = 8 centímetros.
Quinta relação métrica
O produto entre a hipotenusa (a) e a altura (h) de um triângulo retângulo é sempre igual ao produto entre as medidas de seus catetos.
ah = bc
Exemplo:
Qual é a área de um triângulo retângulo cujos lados possuem as seguintes medidas: 10, 8 e 6 centímetros?
Solução:
10 centímetros é a medida do maior lado, portanto, esse é a hipotenusa e os outros dois são catetos. Para encontrar a área, é necessário saber a altura, logo, usaremos essa relação métrica para encontrar a altura desse triângulo e depois calcularemos sua área.
a·h = b·c
10·h = 8·6
10·h = 48
h = 48
10
h = 4,8 centímetros.
A = 10·4,8
2
A = 48
2
A = 24 cm2
Por Luiz Paulo Moreira
Graduado em Matemática

