O teorema de Pitágoras é uma expressão matemática que relaciona os lados de um triângulo retângulo, conhecidos como hipotenusa e catetos. Esse teorema não é válido para triângulos acutângulos ou obtusângulos, apenas para os retângulos.
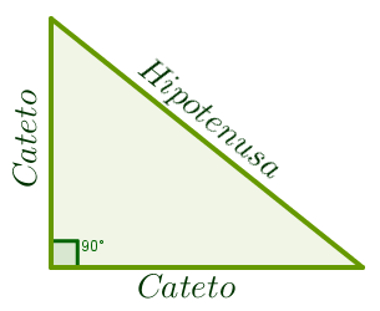
Para que um triângulo seja considerado retângulo, basta que um de seus ângulos tenha medida igual a 90°, ou seja, que o triângulo tenha um ângulo reto. O lado oposto a esse ângulo é o maior lado do triângulo retângulo e é chamado de hipotenusa. Os outros dois lados menores são chamados de catetos, como mostra a figura a seguir:
Tópicos deste artigo
Expressão matemática: Teorema de Pitágoras
O quadrado da hipotenusa é igual à soma dos quadrados dos catetos.
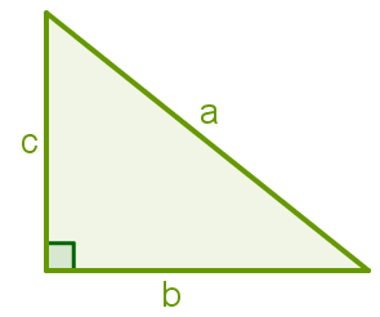
Essa expressão também pode ser representada na forma de equação. Para isso, faça hipotenusa = a, cateto 1 = b e cateto 2 = c. Nessas condições, teremos:
a2 = b2 + c2
Essa é uma fórmula válida para o seguinte triângulo:
Mapa Mental: Teorema de Pitágoras
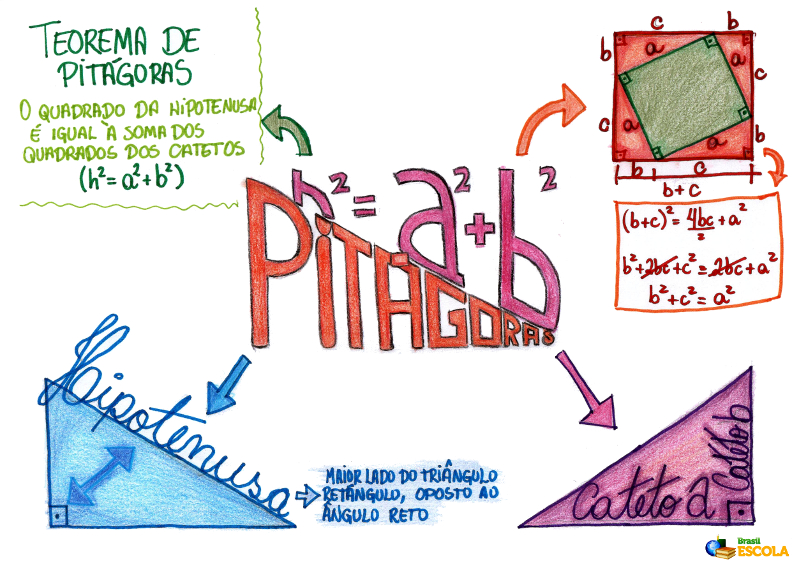
* Baixe o mapa mental sobre teorema de Pitágoras!
Exemplo
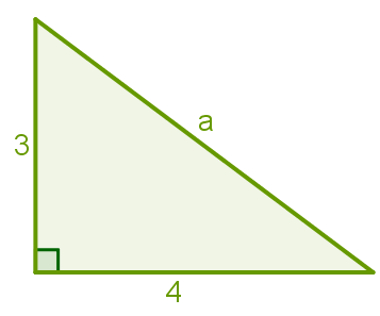
1.Calcule a medida da hipotenusa do triângulo retângulo presente na figura a seguir.
Solução:
Observe que 3 cm e 5 cm são as medidas dos catetos do triângulo acima. A outra medida refere-se ao lado oposto ao ângulo reto, portanto, a hipotenusa. Usando o teorema de Pitágoras, teremos:
a2 = b2 + c2
a2 = 42 + 32
a2 = 16 + 9
a2 = 25
a = √25
a = 5
A hipotenusa desse triângulo mede 5 centímetros.
2. O lado oposto ao ângulo reto de um triângulo retângulo mede 15 centímetros e um dos outros dois lados mede 12 centímetros. Calcule a medida do terceiro lado.
Solução:
O lado oposto ao ângulo reto é a hipotenusa. Os outros dois são catetos. Representando o cateto que falta pela letra b, podemos usar o teorema de Pitágoras para descobrir a terceira medida. Basta lembrar que ela também é um cateto. Sendo assim, teremos:
a2 = b2 + c2
152 = b2 + 122
Observe que a medida da hipotenusa foi colocada no lugar da letra a, pois essa letra representa essa medida. Resolvendo a equação, encontraremos o valor de b:
225 = b2 + 144
225 – 144 = b2
81 = b2
b2 = 81
b = √81
b = 9
O terceiro lado mede 9 centímetros.
3. (Enem 2006) Na figura abaixo, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
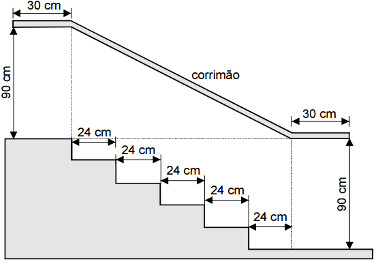
a) 1,8 m.
b) 1,9 m.
c) 2,0 m.
d) 2,1 m.
e) 2,2 m.
Solução:
Observe o seguinte triângulo retângulo sobre o corrimão da imagem do exercício.
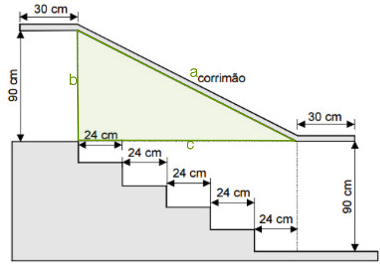
Perceba que o comprimento do corrimão é igual à soma 30 + a + 30 e que “a” é a medida da hipotenusa do triângulo colocado sobre a imagem. Além disso, note que b = 90 e que c = 24 + 24 + 24 + 24 + 24 = 120. Assim, para descobrir a medida de a, faremos:
a2 = b2 + c2
a2 = 902 + 1202
a2 = 8100 + 14400
a2 = 22500
a = √22500
a = 150 centímetros.
A medida do corrimão é 30 + 150 + 30 = 210 cm ou 2,1 m.
Gabarito: letra D.
Por Luiz Paulo Moreira
Graduado em Matemática


