O que é o Teorema de Tales?

Teorema de Tales é como ficou conhecida a propriedade matemática que relaciona as medidas dos segmentos de reta formados por um feixe de retas paralelas cortado por retas transversais. Antes de falar do teorema em si, é bom lembrar o conceito de feixe de retas paralelas, retas transversais e uma de suas propriedades:

Duas ou mais retas são paralelas quando elas não possuem nenhum ponto em comum. Quando destacamos três ou mais retas paralelas em um plano, dizemos que elas formam um feixe de retas paralelas. As retas transversais são aquelas que “cortam” as retas paralelas.

Suponha que um feixe de retas paralelas forme segmentos de reta congruentes sobre uma reta transversal qualquer. Nessa hipótese, ele também forma segmentos congruentes em qualquer outra reta transversal.

A imagem a seguir mostra um feixe de retas paralelas, duas retas transversais e as medidas dos segmentos de reta formados por elas.

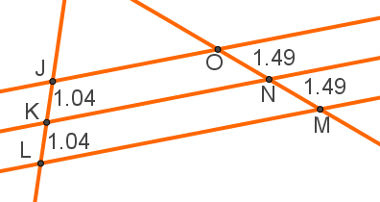
Teorema de Tales

Os segmentos de reta formados sobre retas transversais a um feixe de retas paralelas são proporcionais.

Isso significa que é possível que as divisões entre os comprimentos de alguns segmentos formados nessas circunstâncias tenham o mesmo resultado.

Para compreender melhor o teorema enunciado, observe a imagem a seguir:

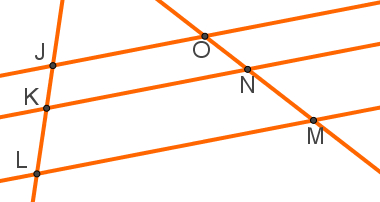
O que o teorema de Tales garante a respeito dos segmentos formados sobre as retas transversais é a seguinte igualdade:

JK = ON
KL   NM

Note que a divisão foi feita, nesse caso, de cima para baixo. Os segmentos superiores nas retas transversais aparecem no numerador. O teorema também garante outras possibilidades. Veja:

 KL = NM
JK    ON

Outras variações podem ser obtidas pela troca das razões de membro ou pela aplicação da propriedade fundamental das proporções (o produto dos meios é igual ao produto dos extremos).

Outras possibilidades de proporcionalidade pelo teorema de tales são:

 JK = KL
ON   NM

ON = NM
JK     KL

JK = ON
JL    OM

KL = NM
JL    OM

Tanto esse teorema quanto essa propriedade são usados para descobrir a medida de um dos segmentos quando se conhece a medida dos outros três ou quando se conhece a razão de proporcionalidade entre dois segmentos. O mais importante para resolver exercícios que envolvem o teorema de Tales é respeitar a ordem em que os segmentos de reta são colocados nas frações.

Exemplos:

• No feixe de retas paralelas a seguir, vamos determinar a medida do segmento NM.

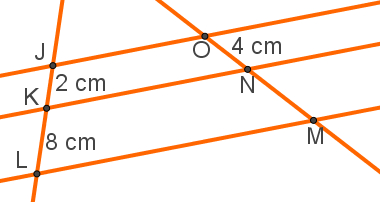
Solução:

Seja x o comprimento do segmento NM, vamos mostrar a proporcionalidade entre os segmentos e utilizar a propriedade fundamental das proporções para resolver a equação:

2 = 4
8    x

2x = 32

x = 32
      2

x = 16 cm.

Note que 8 = 2·4 e que 16 também é igual a 2·4. Isso acontece porque, na configuração utilizada, a razão de proporcionalidade é 1/4. Note também que qualquer uma das razões expostas acima poderia ter sido utilizada para resolver esse problema e o resultado seria o mesmo.

• A partir da imagem a seguir, vamos calcular a medida do segmento JK.

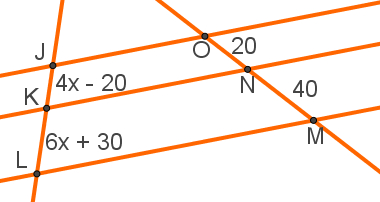
Solução:

Vamos escolher uma das razões descritas no teorema de Tales, substituir os valores dados no exercício e utilizar a propriedade fundamental das proporções, ou seja:

4x – 20 = 20
6x + 30 = 40

40(4x – 20) = 20(6x + 30)

160x – 800 = 120x + 600

160x – 120x = 600 + 800

40x = 1400

x = 1400
     40

x = 35

Para descobrir o comprimento de JK, temos que resolver a seguinte expressão:

JK = 4x – 20

JK = 4·35 – 20

JK = 140 – 20

JK = 120

Por Luiz Paulo Moreira
Graduado em Matemática