O que são ângulos opostos pelo vértice?

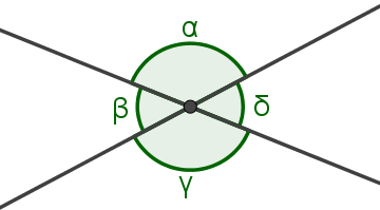
Duas retas concorrentes formam quatro ângulos. Analisados dois a dois, é possível notar que esses ângulos ou estão lado a lado ou só possuem um único ponto em comum, que também é o ponto de encontro das duas retas. Quando dois ângulos possuem essa última característica, eles são chamados de ângulos opostos pelo vértice.

Os outros dois ângulos, que estão lado a lado, são chamados de ângulos adjacentes.

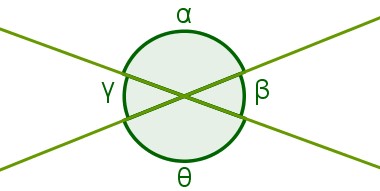
Ângulos opostos pelo vértice e ângulos adjacentes em retas concorrentes

Propriedades

• Ângulos adjacentes são suplementares;

• Ângulos opostos pelo vértice são congruentes, isto é, possuem medidas iguais. Observe os ângulos a seguir:

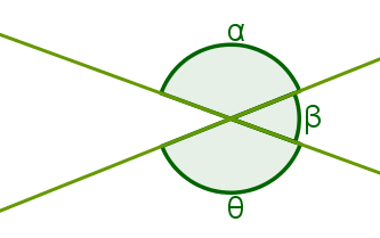
Se α, β e θ são as medidas dos ângulos em questão, as somas α + β e β + θ são iguais a 180° porque os respectivos ângulos são adjacentes. Assim, podemos escrever:

α + β = 180 e β + θ = 180

A partir das duas igualdades acima, podemos escrever o seguinte:

180 = 180

α + β = β + θ

α = β – β + θ

α = θ

Logo, os ângulos opostos pelo vértice são congruentes.

Exemplos

1º) Qual é a medida do ângulo α na figura a seguir?

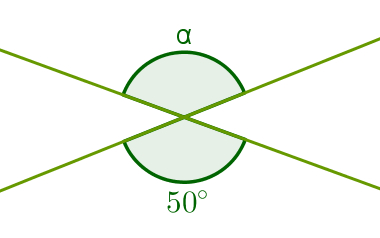
Solução:

Observe que o ângulo de 50° é oposto pelo vértice ao ângulo α, logo, α = 50°.

2º) Calcule a medida de cada ângulo na figura a seguir.

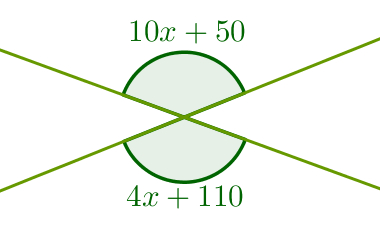
Solução:

Sabendo que ângulos opostos pelo vértice são congruentes, basta observar a seguinte equação:

10x + 50 = 4x + 110

10x – 4x = 110 – 50

6x = 60

x = 60
      6

x = 10

Para descobrir a medida de cada ângulo, basta substituir o valor de x em uma das expressões:

10x + 50 =

10·10 + 50 =

100 + 50 =

150°

Como os ângulos são opostos pelo vértice, o outro ângulo também mede 150°.

Por Luiz Paulo Moreira
Graduado em Matemática