Razão trigonométrica – também chamada de relação trigonométrica – é, grosso modo, o resultado da divisão entre as medidas de dois lados de um triângulo retângulo. As razões trigonométricas são capazes de relacionar os lados com os ângulos de um triângulo retângulo. Se não fosse por elas, só seria possível construir o que conhecemos como relações métricas.
Antes de definir as razões trigonométricas, é importante conhecer a nomenclatura dos lados de um triângulo retângulo.
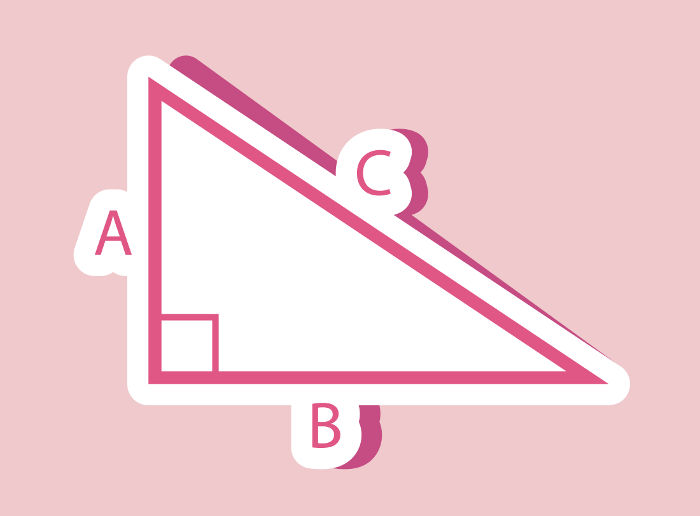
Triângulo retângulo
Em um triângulo retângulo qualquer, o lado oposto ao ângulo reto – que é o maior lado do triângulo – recebe o nome de hipotenusa. Os outros dois recebem o nome de catetos.
Além disso, fixando o ângulo agudo θ de um triângulo retângulo qualquer, o lado oposto a esse ângulo recebe o nome de cateto oposto, e o lado que toca esse ângulo é chamado de cateto adjacente.
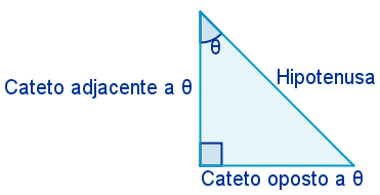
Razões trigonométricas
As razões trigonométricas foram criadas a partir da seguinte observação: Dois triângulos retângulos que possuem um segundo ângulo congruente são semelhantes. Isso significa que, entre esses dois triângulos, as medidas dos lados são proporcionais e as medidas dos ângulos são congruentes. Dessa forma, tomando um ângulo agudo de um triângulo retângulo, a razão entre seus lados terá o mesmo resultado.
Essa informação é importante para a trigonometria porque uma razão trigonométrica relacionada com um determinado ângulo terá um valor fixo para qualquer triângulo, independentemente do tamanho de seus lados, pois, como eles são proporcionais, a razão entre os lados correspondentes será igual.
Dito isso, definiremos as razões trigonométricas seno, cosseno e tangente:
Senθ = Cateto oposto a θ
Hipotenusa
Cosθ = Cateto adjacente a θ
Hipotenusa
Tgθ = Cateto oposto a θ
Cateto adjacente a θ
Um valor para cada ângulo
O seno de um ângulo é invariável independentemente da medida do lado do triângulo de onde esse ângulo foi tirado. O triângulo a seguir foi construído no computador, de modo que possuísse um ângulo reto e outro de 30º, representado pela letra grega θ. As medidas obtidas foram:
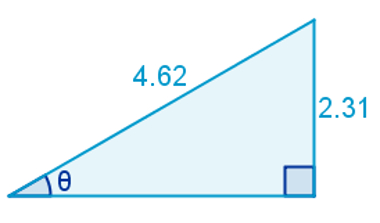
Calculando o seno de 30°, teremos:
Sen30º = Cateto oposto a θ = 2,31 = 0,5
Hipotenusa 4,62
O valor 0,5 é o seno de 30° para qualquer triângulo. Isso acontece porque todos os triângulos que possuem dois ângulos congruentes são proporcionais. Nesse exemplo, 0,5 é justamente a razão de proporção encontrada nos triângulos retângulos que possuem um ângulo de 30°.
Tabela trigonométrica
Os cálculos acima podem ser feitos para todos os ângulos “inteiros” - um ângulo também pode ser fracionado. As frações “decimais” são chamadas de minutos e as “centesimais” são chamadas de segundos. Utilizando as razões seno, cosseno e tangente, seria possível construir a seguinte tabela de valores:
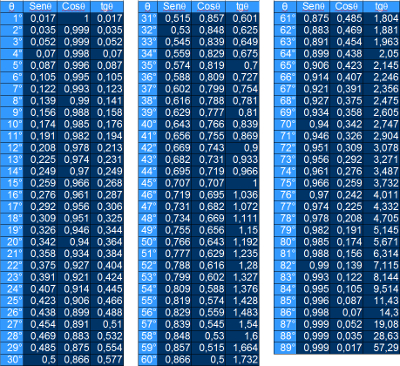
Aplicações práticas
Por meio das razões trigonométricas, é possível relacionar os ângulos de um triângulo retângulo com os valores de seus lados. Logo, é possível descobrir a medida de um lado de um triângulo retângulo dispondo apenas das medidas de um de seus ângulos agudos e de um de seus lados. Observe o exemplo:
Calcule o valor do lado de comprimento a no triângulo seguinte:
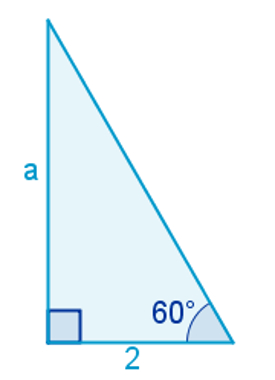
Nesse triângulo, queremos descobrir o valor do cateto oposto ao ângulo de 60° a partir do valor de seu cateto adjacente. Observando as razões trigonométricas definidas acima, observamos que a única que relaciona o cateto oposto ao cateto adjacente é a tangente. Portanto, utilizaremos essa razão para descobrir o valor de “a”. Procurando a tangente de 60° na tabela anterior, encontramos o valor: 1,732. Observe os cálculos utilizados para descobrir a medida do lado a:
Tg60 = Cateto oposto a 60 = a
Cateto adjacente a 60 2
Tg60 = a
2
1,732 = a
2
a = 1,732·2
a = 3,464
Por Luiz Paulo Moreira
Graduado em Matemática