Seno, cosseno e tangente são divisões realizadas entre as medidas de lados de um triângulo retângulo. Elas podem ser usadas para relacionar essas medidas de lados a medidas de ângulos, formando um estudo conhecido como Trigonometria. Essas divisões são conhecidas como razões trigonométricas.
Definição de seno, cosseno e tangente
Se consideramos um triângulo retângulo qualquer e fixamos um dos outros dois ângulos α, temos:
senα = cateto oposto a α
hipotenusa
cosα = cateto adjacente a α
hipotenusa
tgα = cateto oposto a α
cateto adjacente a α
Cateto oposto, cateto adjacente e hipotenusa são os lados do triângulo retângulo. Para compreender melhor essas razões, é importante conhecer bem esses lados como elementos do triângulo retângulo.
Elementos do triângulo retângulo
Para ser chamado triângulo retângulo, esse polígono, necessariamente, precisa ter um ângulo reto. O lado de um triângulo retângulo que se opõe ao ângulo reto é chamado hipotenusa. Esse lado também é o maior desses triângulos. Os outros dois lados são chamados catetos.
Fixando um dos outros dois ângulos (α), poderemos determinar qual dos dois catetos é oposto e qual deles é adjacente a esse ângulo. O cateto que não é um dos lados do ângulo é o cateto oposto. O outro é o cateto adjacente.
A imagem a seguir mostra um exemplo de um triângulo retângulo com seus elementos.
O cateto oposto ao ângulo α é o lado AB, o cateto adjacente é o lado AC e a hipotenusa é o lado BC.
Valores de seno, cosseno e tangente
Seno, cosseno e tangente têm como resultados números reais que variam de acordo com a variação do ângulo α. Dois triângulos retângulos que possuem também um ângulo com a medida α serão obrigatoriamente semelhantes. Assim, os resultados das razões trigonométricas avaliadas nesses dois triângulos serão iguais, já que seus lados são proporcionais.
Assim, independentemente dos comprimentos dos lados de um triângulo retângulo que possui um ângulo de 30°, por exemplo, o seno de 30° sempre será igual a 1/2, pois, em um triângulo retângulo que possui um ângulo de 30°, a hipotenusa tem o dobro do comprimento do cateto oposto a esse ângulo.
A tabela a seguir mostra os valores de seno cosseno e tangente dos ângulos notáveis, isto é, dos ângulos de 30°, 45° e 60°.
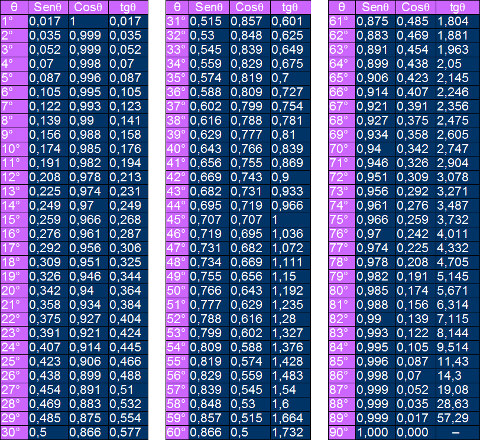
Esses valores podem ser encontrados por meio de cálculos nos quais conhecemos as medidas dos ângulos internos de um triângulo e de seus lados. Todo ângulo no intervalo de 1° a 89° possui valores de seno, cosseno e tangente. Esses valores podem ser encontrados na tabela completa a seguir:
Por Luiz Paulo Moreira
Graduado em Matemática

.jpg)
.jpg)