O que é função?

Função é uma regra que relaciona cada elemento de um conjunto (representado pela variável x) a um único elemento de outro conjunto (representado pela variável y). Para cada valor de x, podemos determinar um valor de y, dizemos então que “y está em função de x”.

Vamos representar uma função de números naturais de forma que, para cada número natural escolhido, obtenha-se o seu dobro. Por exemplo, se escolhermos o 1, teremos o número 2; se escolhermos o 2, teremos o 4; se escolhermos o 3, teremos o 6 e assim por diante. Podemos representar uma função utilizando o diagrama de flechas ou o diagrama de setas, como na figura a seguir:

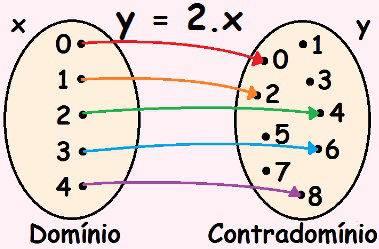
O Diagrama de flechas ou diagrama de setas é usado para representar funções

Nessa representação há dois conjuntos numéricos, um domínio e um contradomínio. Dentro do contradomínio há um subconjunto chamado de imagem. Esse subconjunto é composto pelos elementos que estão recebendo a seta, isto é, aqueles que possuem alguma relação com os elementos do domínio. Ao trabalharmos com funções, sempre teremos uma “lei da função” que determinará como serão os elementos da imagem dessa função. Nesse caso, há uma função de y em relação a x, uma vez que, para cada x escolhido, há um y. Dizemos ainda que y é a variável dependente e, por sua vez, que x é a variável independente.

Se os elementos do domínio e da imagem de uma função pertencem ao conjunto dos números inteiros, por exemplo, dizemos que f: → , lemos que “f é uma função cujo domínio pertence aos inteiros e cuja imagem pertence aos inteiros” ou, simplesmente, “f é uma função de inteiros em inteiros”.

As funções podem ser classificadas da seguinte forma:

• Função sobrejetora

  Dizemos que uma função é sobrejetora se todos os elementos do contradomínio pertencem ao conjunto da imagem, isto é, se todos os elementos “recebem uma seta vinda do domínio, ou, simplesmente, se o conjunto da imagem e do contradomínio são iguais.” Um mesmo elemento do contradomínio pode receber uma correspondência de mais de um elemento do domínio.

• Função Injetora

  Uma função é dita injetora se cada elemento do domínio possuir uma única e distinta imagem, isto é, um elemento do conjunto da imagem pode corresponder a dois elementos do domínio.

• Função Bijetora

  Uma função é bijetora se ela for sobrejetora e injetora simultaneamente, isto é, se todos os elementos do contradomínio pertencem ao conjunto da imagem e um elemento do contradomínio corresponde a um único elemento do domínio.

• Função Simples

  Uma função é dita simples se ela não é injetora nem sobrejetora.

No esquema a seguir há uma representação de cada tipo de função utilizando o diagrama de flechas:

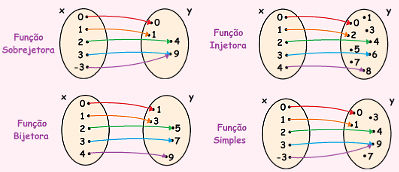
Cada tipo de função possui uma regularidade especifica

Por Amanda Gonçalves
Graduada em Matemática